 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
This module contains main algorithms to solve boundary element method problems in 3 dimensional space. More...
Data Structures | |
| struct | _bem3d |
| Main container object for computation of BEM related matrices and vectors. More... | |
| struct | _kernelbem3d |
| Substructure containing callback functions to different types of kernel evaluations. More... | |
| struct | _listnode |
| simple singly linked list to store unsigned inter values. More... | |
| struct | _tri_list |
| Simple singly connected list to efficiently store a list of triangles. More... | |
| struct | _vert_list |
| Simple singly connected list to efficiently store a list of vertices. More... | |
Typedefs | |
| typedef struct _bem3d | bem3d |
| typedef bem3d * | pbem3d |
| typedef const bem3d * | pcbem3d |
| typedef struct _aprxbem3d | aprxbem3d |
| typedef aprxbem3d * | paprxbem3d |
| typedef const aprxbem3d * | pcaprxbem3d |
| typedef struct _parbem3d | parbem3d |
| typedef parbem3d * | pparbem3d |
| typedef const parbem3d * | pcparbem3d |
| typedef struct _kernelbem3d | kernelbem3d |
| typedef kernelbem3d * | pkernelbem3d |
| typedef const kernelbem3d * | pckernelbem3d |
| typedef void(* | quadpoints3d) (pcbem3d bem, const real bmin[3], const real bmax[3], const real delta, real(**Z)[3], real(**N)[3]) |
| Callback function type for parameterizations. More... | |
| typedef enum _basisfunctionbem3d | basisfunctionbem3d |
| typedef field(* | boundary_func3d) (const real *x, const real *n, void *data) |
| typedef field(* | kernel_func3d) (const real *x, const real *y, const real *nx, const real *ny, void *data) |
Evaluate a fundamental solution or its normal derivatives at points x and y. More... | |
| typedef field(* | kernel_wave_func3d) (const real *x, const real *y, const real *nx, const real *ny, pcreal dir, void *data) |
Evaluate a modified fundamental solution or its normal derivatives at points x and y. More... | |
| typedef struct _listnode | listnode |
| typedef listnode * | plistnode |
| typedef struct _tri_list | tri_list |
| typedef tri_list * | ptri_list |
| typedef struct _vert_list | vert_list |
| typedef vert_list * | pvert_list |
Enumerations | |
| enum | _basisfunctionbem3d { BASIS_NONE_BEM3D = 0, BASIS_CONSTANT_BEM3D = 'c', BASIS_LINEAR_BEM3D = 'l' } |
| Possible types of basis functions. More... | |
Functions | |
| pvert_list | new_vert_list (pvert_list next) |
| Create a new list to store a number of vertex indices. More... | |
| void | del_vert_list (pvert_list vl) |
| Recursively deletes a vert_list. More... | |
| ptri_list | new_tri_list (ptri_list next) |
| Create a new list to store a number of triangles indices. More... | |
| void | del_tri_list (ptri_list tl) |
| Recursively deletes a tri_list. More... | |
| pbem3d | new_bem3d (pcsurface3d gr, basisfunctionbem3d row_basis, basisfunctionbem3d col_basis) |
| Main constructor for bem3d objects. More... | |
| void | del_bem3d (pbem3d bem) |
| Destructor for bem3d objects. More... | |
| pclustergeometry | build_bem3d_const_clustergeometry (pcbem3d bem, uint **idx) |
| Creates a clustergeometry object for a BEM-Problem using piecewise constant basis functions. More... | |
| pclustergeometry | build_bem3d_linear_clustergeometry (pcbem3d bem, uint **idx) |
| Creates a clustergeometry object for a BEM-Problem using linear basis functions. More... | |
| pclustergeometry | build_bem3d_clustergeometry (pcbem3d bem, uint **idx, basisfunctionbem3d basis) |
| Creates a clustergeometry object for a BEM-Problem using the type of basis functions specified by basis. More... | |
| pcluster | build_bem3d_cluster (pcbem3d bem, uint clf, basisfunctionbem3d basis) |
| Creates a clustertree for specified basis functions. More... | |
| void | assemble_cc_near_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise constant basis functions for both Ansatz and test functions. More... | |
| void | assemble_cc_far_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise constant basis functions for both Ansatz and test functions. More... | |
| void | assemble_cl_near_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise constant basis functions for Test and piecewise linear basis functions for Ansatz functions. More... | |
| void | assemble_cl_far_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise constant basis functions for Test and piecewise linear basis functions for Ansatz functions. More... | |
| void | assemble_lc_near_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise linear basis functions for Test and piecewise contant basis functions for Ansatz functions. More... | |
| void | assemble_lc_far_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise linear basis functions for Test and piecewise contant basis functions for Ansatz functions. More... | |
| void | assemble_ll_near_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise linear basis functions for both Ansatz and test functions. More... | |
| void | assemble_ll_far_bem3d (const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N, kernel_func3d kernel) |
| Compute general entries of a boundary integral operator with piecewise linear basis functions for both Ansatz and test functions. More... | |
| void | fill_bem3d (pcbem3d bem, const real(*X)[3], const real(*Y)[3], const real(*NX)[3], const real(*NY)[3], pamatrix V, kernel_func3d kernel) |
Evaluate a kernel function  at some points at some points  and and  . More... . More... | |
| void | fill_wave_bem3d (pcbem3d bem, const real(*X)[3], const real(*Y)[3], const real(*NX)[3], const real(*NY)[3], pamatrix V, pcreal dir, kernel_wave_func3d kernel) |
Evaluate a modified kernel function  at some points at some points  and and  for some direction for some direction 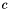 . More... . More... | |
| void | fill_row_c_bem3d (const uint *idx, const real(*Z)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a kernel function  on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_col_c_bem3d (const uint *idx, const real(*Z)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a kernel function  on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_row_l_bem3d (const uint *idx, const real(*Z)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a kernel function  on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_col_l_bem3d (const uint *idx, const real(*Z)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a kernel function  on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_dnz_row_c_bem3d (const uint *idx, const real(*Z)[3], const real(*N)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a normal derivative of a kernel function  with respect to with respect to 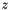 on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_dnz_col_c_bem3d (const uint *idx, const real(*Z)[3], const real(*N)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a normal derivative of a kernel function  with respect to with respect to 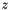 on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_dnz_row_l_bem3d (const uint *idx, const real(*Z)[3], const real(*N)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a normal derivative of a kernel function  with respect to with respect to 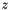 on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | fill_dnz_col_l_bem3d (const uint *idx, const real(*Z)[3], const real(*N)[3], pcbem3d bem, pamatrix V, kernel_func3d kernel) |
This function will integrate a normal derivative of a kernel function  with respect to with respect to 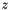 on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points  will be used. The results will be stored in a matrix will be used. The results will be stored in a matrix V. More... | |
| void | setup_hmatrix_recomp_bem3d (pbem3d bem, bool recomp, real accur_recomp, bool coarsen, real accur_coarsen) |
| Initialize the bem object for on the fly recompression techniques. More... | |
| void | setup_hmatrix_aprx_inter_row_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m) |
| This function initializes the bem3d object for approximating a matrix with tensorinterpolation within the row cluster. More... | |
| void | setup_hmatrix_aprx_inter_col_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m) |
| This function initializes the bem3d object for approximating a matrix with tensorinterpolation within the column cluster. More... | |
| void | setup_hmatrix_aprx_inter_mixed_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m) |
| This function initializes the bem3d object for approximating a matrix with tensorinterpolation within one of row or column cluster. More... | |
| void | setup_hmatrix_aprx_green_row_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, quadpoints3d quadpoints) |
| creating hmatrix approximation using green's method with row cluster . More... | |
| void | setup_hmatrix_aprx_green_col_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, quadpoints3d quadpoints) |
| creating hmatrix approximation using green's method with column cluster . More... | |
| void | setup_hmatrix_aprx_green_mixed_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, quadpoints3d quadpoints) |
| creating hmatrix approximation using green's method with one of row or column cluster . More... | |
| void | setup_hmatrix_aprx_greenhybrid_row_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, real accur, quadpoints3d quadpoints) |
| creating hmatrix approximation using green's method with row cluster connected with recompression technique using ACA. More... | |
| void | setup_hmatrix_aprx_greenhybrid_col_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, real accur, quadpoints3d quadpoints) |
| creating hmatrix approximation using green's method with column cluster connected with recompression technique using ACA. More... | |
| void | setup_hmatrix_aprx_greenhybrid_mixed_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, real accur, quadpoints3d quadpoints) |
| creating hmatrix approximation using green's method with row or column cluster connected with recompression technique using ACA. More... | |
| void | setup_hmatrix_aprx_aca_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, real accur) |
| Approximate matrix block with ACA using full pivoting. More... | |
| void | setup_hmatrix_aprx_paca_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, real accur) |
| Approximate matrix block with ACA using partial pivoting. More... | |
| void | setup_hmatrix_aprx_hca_bem3d (pbem3d bem, pccluster rc, pccluster cc, pcblock tree, uint m, real accur) |
| Approximate matrix block with hybrid cross approximation using Interpolation and ACA with full pivoting. More... | |
| void | setup_h2matrix_recomp_bem3d (pbem3d bem, bool hiercomp, real accur_hiercomp) |
| Enables hierarchical recompression for hmatrices. More... | |
| void | setup_h2matrix_aprx_inter_bem3d (pbem3d bem, pcclusterbasis rb, pcclusterbasis cb, pcblock tree, uint m) |
| Initialize the bem3d object for approximating a h2matrix with tensorinterpolation. More... | |
| void | setup_h2matrix_aprx_greenhybrid_bem3d (pbem3d bem, pcclusterbasis rb, pcclusterbasis cb, pcblock tree, uint m, uint l, real delta, real accur, quadpoints3d quadpoints) |
| Initialize the bem3d object for approximating a h2matrix with green's method and ACA based recompression. More... | |
| void | setup_h2matrix_aprx_greenhybrid_ortho_bem3d (pbem3d bem, pcclusterbasis rb, pcclusterbasis cb, pcblock tree, uint m, uint l, real delta, real accur, quadpoints3d quadpoints) |
| Initialize the bem3d object for approximating a h2matrix with green's method and ACA based recompression. The resulting clusterbasis will be orthogonal. More... | |
| void | setup_dh2matrix_aprx_inter_bem3d (pbem3d bem, pcdclusterbasis rb, pcdclusterbasis cb, pcdblock tree, uint m) |
Initialize the bem3d object for an interpolation based 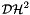 -matrix approximation. More... -matrix approximation. More... | |
| void | setup_dh2matrix_aprx_inter_ortho_bem3d (pbem3d bem, pcdclusterbasis rb, pcdclusterbasis cb, pcdblock tree, uint m) |
Initialize the bem3d object for an interpolation based 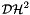 -matrix approximation with orthogonal directional cluster basis. More... -matrix approximation with orthogonal directional cluster basis. More... | |
| void | setup_dh2matrix_aprx_inter_recomp_bem3d (pbem3d bem, pcdclusterbasis rb, pcdclusterbasis cb, pcdblock tree, uint m, ptruncmode tm, real eps) |
Initialize the bem3d object for an interpolation based 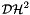 -matrix approximation with orthogonal directional cluster basis. During the filling process the -matrix approximation with orthogonal directional cluster basis. During the filling process the 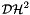 -matrix will be recompressed with respective to truncmode and the given accuracy -matrix will be recompressed with respective to truncmode and the given accuracy eps. More... | |
| void | assemble_bem3d_amatrix (pbem3d bem, pamatrix G) |
Assemble a dense matrix for some boundary integral operator given by bem. More... | |
| void | assemble_bem3d_hmatrix (pbem3d bem, pblock b, phmatrix G) |
| Fills a hmatrix with a predefined approximation technique. More... | |
| void | assemblecoarsen_bem3d_hmatrix (pbem3d bem, pblock b, phmatrix G) |
| Fills a hmatrix with a predefined approximation technique using coarsening strategy. More... | |
| void | assemble_bem3d_nearfield_hmatrix (pbem3d bem, pblock b, phmatrix G) |
| Fills the nearfield blocks of a hmatrix. More... | |
| void | assemble_bem3d_farfield_hmatrix (pbem3d bem, pblock b, phmatrix G) |
| Fills the farfield blocks of a hmatrix with a predefined approximation technique. More... | |
| void | assemble_bem3d_h2matrix_row_clusterbasis (pcbem3d bem, pclusterbasis rb) |
This function computes the matrix entries for the nested clusterbasis  . More... . More... | |
| void | assemble_bem3d_h2matrix_col_clusterbasis (pcbem3d bem, pclusterbasis cb) |
This function computes the matrix entries for the nested clusterbasis  . More... . More... | |
| void | assemble_bem3d_h2matrix (pbem3d bem, ph2matrix G) |
| Fills a h2matrix with a predefined approximation technique. More... | |
| void | assemble_bem3d_nearfield_h2matrix (pbem3d bem, ph2matrix G) |
| Fills the nearfield part of a h2matrix. More... | |
| void | assemble_bem3d_farfield_h2matrix (pbem3d bem, ph2matrix G) |
| Fills a h2matrix with a predefined approximation technique. More... | |
| void | assemblehiercomp_bem3d_h2matrix (pbem3d bem, pblock b, ph2matrix G) |
| Fills an h2matrix with a predefined approximation technique using hierarchical recompression. More... | |
| void | assemble_bem3d_dh2matrix_row_dclusterbasis (pcbem3d bem, pdclusterbasis rb) |
This function computes the matrix entries for the nested dclusterbasis  . More... . More... | |
| void | assemble_bem3d_dh2matrix_col_dclusterbasis (pcbem3d bem, pdclusterbasis cb) |
This function computes the matrix entries for the nested dclusterbasis  . More... . More... | |
| void | assemble_bem3d_dh2matrix_ortho_row_dclusterbasis (pcbem3d bem, pdclusterbasis rb, pdclusteroperator ro) |
| Function for filling a directional row cluster basis with orthogonal matrices. More... | |
| void | assemble_bem3d_dh2matrix_ortho_col_dclusterbasis (pcbem3d bem, pdclusterbasis cb, pdclusteroperator co) |
| Function for filling a directional column cluster basis with orthogonal matrices. More... | |
| void | assemble_bem3d_dh2matrix_recomp_both_dclusterbasis (pcbem3d bem, pdclusterbasis rb, pdclusteroperator bro, pdclusterbasis cb, pdclusteroperator bco, pcdblock broot) |
| Function for filling both directional cluster bases with orthogonal matrices. More... | |
| void | assemble_bem3d_dh2matrix (pbem3d bem, pdh2matrix G) |
| Fills a dh2matrix with a predefined approximation technique. More... | |
| void | assemble_bem3d_nearfield_dh2matrix (pbem3d bem, pdh2matrix G) |
| Fills the nearfield part of a dh2matrix. More... | |
| void | assemble_bem3d_farfield_dh2matrix (pbem3d bem, pdh2matrix G) |
| Fills a dh2matrix with a predefined approximation technique. More... | |
| void | assemble_bem3d_lagrange_c_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcbem3d bem, pamatrix V) |
This function will integrate Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_lagrange_wave_c_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcreal dir, pcbem3d bem, pamatrix V) |
This function will integrate modified Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_lagrange_l_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcbem3d bem, pamatrix V) |
This function will integrate Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_lagrange_wave_l_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcreal dir, pcbem3d bem, pamatrix V) |
This function will integrate modified Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_dn_lagrange_c_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcbem3d bem, pamatrix V) |
This function will integrate the normal derivatives of the Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_dn_lagrange_wave_c_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcreal dir, pcbem3d bem, pamatrix V) |
This function will integrate the normal derivatives of the modified Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_dn_lagrange_l_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcbem3d bem, pamatrix V) |
This function will integrate the normal derivatives of the Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_dn_lagrange_wave_l_amatrix (const uint *idx, pcrealavector px, pcrealavector py, pcrealavector pz, pcreal dir, pcbem3d bem, pamatrix V) |
This function will integrate the normal derivatives of the modified Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V. More... | |
| void | assemble_bem3d_lagrange_amatrix (const real(*X)[3], pcrealavector px, pcrealavector py, pcrealavector pz, pcbem3d bem, pamatrix V) |
This function will evaluate the Lagrange polynomials in a given point set X and store the results in a matrix V. More... | |
| void | assemble_bem3d_lagrange_wave_amatrix (const real(*X)[3], pcrealavector px, pcrealavector py, pcrealavector pz, pcreal dir, pcbem3d bem, pamatrix V) |
This function will evaluate the modified Lagrange polynomials in a given point set X and store the results in a matrix V. More... | |
| real | normL2_bem3d (pbem3d bem, boundary_func3d f, void *data) |
Compute the  -norm of some given function -norm of some given function f. More... | |
| real | normL2_c_bem3d (pbem3d bem, pavector x) |
Compute the  -norm of some given function -norm of some given function  in terms of a piecewise constant basis in terms of a piecewise constant basis  . More... . More... | |
| real | normL2diff_c_bem3d (pbem3d bem, pavector x, boundary_func3d f, void *data) |
Compute the  difference norm of some given function difference norm of some given function  in terms of a piecewise constant basis in terms of a piecewise constant basis  and some other function and some other function  . More... . More... | |
| real | normL2_l_bem3d (pbem3d bem, pavector x) |
Compute the  -norm of some given function -norm of some given function  in terms of a piecewise linear basis in terms of a piecewise linear basis  . More... . More... | |
| real | normL2diff_l_bem3d (pbem3d bem, pavector x, boundary_func3d f, void *data) |
Compute the  difference norm of some given function difference norm of some given function  in terms of a piecewise linear basis in terms of a piecewise linear basis  and some other function and some other function  . More... . More... | |
| void | integrate_bem3d_c_avector (pbem3d bem, boundary_func3d f, pavector w, void *data) |
| Computes the integral of a given function using piecewise constant basis functions over the boundary of a domain. More... | |
| void | integrate_bem3d_l_avector (pbem3d bem, boundary_func3d f, pavector w, void *data) |
| Computes the integral of a given function using piecewise linear basis functions over the boundary of a domain. More... | |
| void | projectL2_bem3d_c_avector (pbem3d bem, boundary_func3d f, pavector w, void *data) |
Computes the  -projection of a given function using piecewise constant basis functions over the boundary of a domain. More... -projection of a given function using piecewise constant basis functions over the boundary of a domain. More... | |
| void | projectL2_bem3d_l_avector (pbem3d bem, boundary_func3d f, pavector w, void *data) |
Computes the  -projection of a given function using linear basis functions over the boundary of a domain. More... -projection of a given function using linear basis functions over the boundary of a domain. More... | |
| void | setup_vertex_to_triangle_map_bem3d (pbem3d bem) |
initializes the field bem->v2t when using linear basis functions More... | |
| void | build_bem3d_cube_quadpoints (pcbem3d bem, const real a[3], const real b[3], const real delta, real(**Z)[3], real(**N)[3]) |
| Generating quadrature points, weights and normal vectors on a cube parameterization. More... | |
| prkmatrix | build_bem3d_rkmatrix (pccluster row, pccluster col, void *data) |
For a block defined by row and col this function will build a rank-k-approximation and return the rkmatrix. More... | |
| pamatrix | build_bem3d_amatrix (pccluster row, pccluster col, void *data) |
For a block defined by row and col this function will compute the full submatrix and return an amatrix. More... | |
| void | build_bem3d_curl_sparsematrix (pcbem3d bem, psparsematrix *C0, psparsematrix *C1, psparsematrix *C2) |
| Set up the surface curl operator. More... | |
This module contains main algorithms to solve boundary element method problems in 3 dimensional space.
bem3d provides basic functionality for a general BEM-application. Considering a special problem such as the Laplace-equation one has to include the laplacebem3d module, which provides the essential quadrature routines of the kernel functions. The bem3d module consists of a struct called bem3d, which contains a collection of callback functions, that regulates the whole computation of fully-populated BEM-matrices and also of h- and h2-matrices.
| typedef struct _aprxbem3d aprxbem3d |
aprxbem3d is just an abbreviation for the struct _aprxbem3d hidden inside the bem3d.c file. This struct is necessary because of the different approximation techniques offered by this library. It will hide all dispensable information from the user.
| typedef enum _basisfunctionbem3d basisfunctionbem3d |
This is just an abbreviation for the enum _basisfunctionbem3d .
Defining a type for function that map from the boundary  of the domain to a field
of the domain to a field  .
.
This type is used to define functions that produce example dirichlet and neumann data.
| x | 3D-point the boundary  . . |
| n | Corresponding outpointing normal vector to x. |
| data | Additional data for evaluating the functional. |
x with normal vector n. | typedef field(* kernel_func3d) (const real *x, const real *y, const real *nx, const real *ny, void *data) |
Evaluate a fundamental solution or its normal derivatives at points x and y.
| x | First evaluation point. |
| y | Second evaluation point. |
| nx | Normal vector that belongs to x. |
| ny | Normal vector that belongs to y. |
| data | Additional data that is needed to evaluate the function. |
| typedef field(* kernel_wave_func3d) (const real *x, const real *y, const real *nx, const real *ny, pcreal dir, void *data) |
Evaluate a modified fundamental solution or its normal derivatives at points x and y.
The modified fundamental solution is defined as
![\[ g_{c}(x,y) = g(x,y) e^{\langle c, x - y \rangle} \]](../../form_317.png)
| x | First evaluation point. |
| y | Second evaluation point. |
| nx | Normal vector that belongs to x. |
| ny | Normal vector that belongs to y. |
| dir | A vector containing the direction 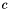 . . |
| data | Additional data that is needed to evaluate the function. |
| typedef struct _kernelbem3d kernelbem3d |
kernelbem3d is just an abbreviation for the struct _kernelbem3d. It contains a collection of callback functions to evaluate or integrate kernel function and its derivatives.
| typedef aprxbem3d* paprxbem3d |
Pointer to a aprxbem3d object.
| typedef struct _parbem3d parbem3d |
parbem3d is just an abbreviation for the struct _parbem3d , which is hidden inside the bem3d.c . It is necessary for parallel computation on h- and h2matrices.
| typedef const aprxbem3d* pcaprxbem3d |
Pointer to a constant aprxbem3d object.
| typedef const kernelbem3d* pckernelbem3d |
Pointer to a constant kernelbem3d object.
| typedef const parbem3d* pcparbem3d |
Pointer to a constant parbem3d object.
| typedef kernelbem3d* pkernelbem3d |
Pointer to a kernelbem3d object.
| typedef vert_list* pvert_list |
Pointer to a vert_list object.
| typedef void(* quadpoints3d) (pcbem3d bem, const real bmin[3], const real bmax[3], const real delta, real(**Z)[3], real(**N)[3]) |
Callback function type for parameterizations.
quadpoints3d defines a class of callback functions that are used to compute quadrature points, weight and normal vectors corresponding to the points on a given parameterization, which are used within the green's approximation functions. The parameters are in ascending order:
| bem | Reference to the bem3d object. |
| bmin | A 3D-array determining the minimal spatial dimensions of the bounding box the parameterization is located around. |
| bmax | A 3D-array determining the maximal spatial dimensions of the bounding box the parameterization is located around. |
| delta | Defines the distant between bounding box and the parameterization. |
| Z | The quadrature points will be stored inside of Z . |
| N | The outer normal vectors will be stored inside of N . For a quadrature point  , a corresponding quadrature weight , a corresponding quadrature weight  and the proper normal vector and the proper normal vector  the vector will not have unit length but the vector will not have unit length but  . . |
| typedef struct _vert_list vert_list |
This is just an abbreviation for the struct _vert_list .
| enum _basisfunctionbem3d |
Possible types of basis functions.
This enum defines all possible values usable for basis functions for either neumann- and dirichlet-data. The values should be self-explanatory.
| void assemble_bem3d_dh2matrix | ( | pbem3d | bem, |
| pdh2matrix | G | ||
| ) |
Fills a dh2matrix with a predefined approximation technique.
This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix  is computed or a duniform rank-k-approximation specified within the bem3d object is created as
is computed or a duniform rank-k-approximation specified within the bem3d object is created as 
 and
and  have to be computed before calling this function because some approximation schemes depend on information residing within the dclusterbasis.
have to be computed before calling this function because some approximation schemes depend on information residing within the dclusterbasis.| void assemble_bem3d_dh2matrix_col_dclusterbasis | ( | pcbem3d | bem, |
| pdclusterbasis | cb | ||
| ) |
This function computes the matrix entries for the nested dclusterbasis  .
.
This algorithm completely traverses the clustertree belonging to the given dclusterbasis until it reaches its leafs. In each leaf cluster the matrix  for all
for all 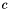 will be constructed and stored within the dclusterbasis. In non leaf clusters the transfer matrices
will be constructed and stored within the dclusterbasis. In non leaf clusters the transfer matrices  for all
for all 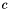 will be computed and it holds
will be computed and it holds
![\[ W_{s,c} = \begin{pmatrix} W_{s_1,\operatorname{sondir}(c)} & & \\ & \ddots & \\ & & W_{s_\sigma, \operatorname{sondir}(c)} \end{pmatrix} \begin{pmatrix} F_{s_1, \operatorname{sondir}(c)} \\ \vdots \\ F_{s_\sigma, \operatorname{sondir}(c)} \end{pmatrix} \]](../../form_345.png)
All matrices  will be stored within the dclusterbasis belonging to the
will be stored within the dclusterbasis belonging to the  -th son.
-th son.
| bem | bem3d object containing all necessary information for computing the entries of clusterbasis cb . |
| cb | Column clusterbasis to be filled. |
| void assemble_bem3d_dh2matrix_ortho_col_dclusterbasis | ( | pcbem3d | bem, |
| pdclusterbasis | cb, | ||
| pdclusteroperator | co | ||
| ) |
Function for filling a directional column cluster basis with orthogonal matrices.
After filling the cluster basis according to the choosen order of interpolation, the matrices will be orthogonalized. The cluster operator is filled with the matrices, which describes the basis change.
| bem | Corresponding bem3d object filled with the needed parameters and callback functions. |
| cb | Directional column cluster basis. |
| co | dclusteroperator object corresponding to cb . |
| void assemble_bem3d_dh2matrix_ortho_row_dclusterbasis | ( | pcbem3d | bem, |
| pdclusterbasis | rb, | ||
| pdclusteroperator | ro | ||
| ) |
Function for filling a directional row cluster basis with orthogonal matrices.
After filling the cluster basis according to the choosen order of interpolation, the matrices will be orthogonalized. The cluster operator is filled with the matrices, which describes the basis change.
| bem | Corresponding bem3d object filled with the needed parameters and callback functions. |
| rb | Directional row cluster basis. |
| ro | dclusteroperator object corresponding to rb . |
| void assemble_bem3d_dh2matrix_recomp_both_dclusterbasis | ( | pcbem3d | bem, |
| pdclusterbasis | rb, | ||
| pdclusteroperator | bro, | ||
| pdclusterbasis | cb, | ||
| pdclusteroperator | bco, | ||
| pcdblock | broot | ||
| ) |
Function for filling both directional cluster bases with orthogonal matrices.
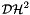 -matrix is filled!
-matrix is filled!After filling the cluster basis according to the choosen order of interpolation, the matrices will be truncated according to the truncation mode and accuracy given in the bem object. The transfer matrices describing the basis change are saved in the two dclusteroperator obejcts bro and bco for filling the 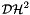 -matrix later.
-matrix later.
| bem | Corresponding bem3d object filled with the needed parameters and callback functions. |
| rb | Directional row cluster basis. |
| bro | dclusteroperator object corresponding to rb. |
| cb | Directional column cluster basis. |
| bco | dclusteroperator object corresponding to cb. |
| broot | dblock object for the corresponding 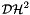 -matrix. -matrix. |
| void assemble_bem3d_dh2matrix_row_dclusterbasis | ( | pcbem3d | bem, |
| pdclusterbasis | rb | ||
| ) |
This function computes the matrix entries for the nested dclusterbasis  .
.
This algorithm completely traverses the clustertree belonging to the given dclusterbasis until it reaches its leafs. In each leaf cluster the matrices  for all
for all 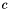 will be constructed and stored within the dclusterbasis. In non leaf clusters the transfer matrices
will be constructed and stored within the dclusterbasis. In non leaf clusters the transfer matrices  for all
for all 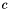 will be computed and it holds
will be computed and it holds
![\[ V_{t,c} = \begin{pmatrix} V_{t_1, \operatorname{sondir}(c)} & & \\ & \ddots & \\ & & V_{t_\tau, \operatorname{sondir}(c)} \end{pmatrix} \begin{pmatrix} E_{t_1, \operatorname{sondir}(c)} \\ \vdots \\ E_{t_\tau, \operatorname{sondir}(c)} \end{pmatrix} \]](../../form_341.png)
All matrices  will be stored within the dclusterbasis belonging to the
will be stored within the dclusterbasis belonging to the  -th son.
-th son.
| bem | bem3d object containing all necessary information for computing the entries of dclusterbasis rb . |
| rb | Row dclusterbasis to be filled. |
| void assemble_bem3d_dn_lagrange_c_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate the normal derivatives of the Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial \mathcal L_\mu}{\partial n} (\vec x) \, \mathrm d \vec x \]](../../form_235.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_dn_lagrange_l_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate the normal derivatives of the Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial \mathcal L_\mu}{\partial n} (\vec x) \, \mathrm d \vec x \]](../../form_235.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_dn_lagrange_wave_c_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcreal | dir, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate the normal derivatives of the modified Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial \mathcal L_{\mu, c}}{\partial n} (\vec x) \, \mathrm d \vec x = \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial}{\partial n} \left(\mathcal L_\mu (\vec x) \, e^{\langle c, \vec x \rangle} \right) \, \mathrm d \vec x \]](../../form_350.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| dir | Direction vector for the direction 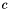 . . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_dn_lagrange_wave_l_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcreal | dir, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate the normal derivatives of the modified Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial \mathcal L_{\mu, c}}{\partial n} (\vec x) \, \mathrm d \vec x = \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial}{\partial n} \left( \mathcal L_\mu (\vec x) \, e^{\langle c, \vec x \rangle} \right) \, \mathrm d \vec x \]](../../form_351.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| dir | Direction vector for the direction 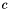 . . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_farfield_dh2matrix | ( | pbem3d | bem, |
| pdh2matrix | G | ||
| ) |
Fills a dh2matrix with a predefined approximation technique.
This will traverse the block tree until it reaches its leafs. For an admissible leaf block a duniform rank-k-approximation specified within the bem3d object is created as 
 and
and  have to be computed before calling this function because some approximation schemes depend on information residing within the dclusterbasis.
have to be computed before calling this function because some approximation schemes depend on information residing within the dclusterbasis.Fills a h2matrix with a predefined approximation technique.
This will traverse the block tree until it reaches its leafs. For an admissible leaf block a uniform rank-k-approximation specified within the bem3d object is created as 
 and
and  have to be computed before calling this function because some approximation schemes depend on information residing within the clusterbasis.
have to be computed before calling this function because some approximation schemes depend on information residing within the clusterbasis.Fills the farfield blocks of a hmatrix with a predefined approximation technique.
This will traverse the block tree until it reaches its leafs. For an admissible leaf block a rank-k-approximation specified within the bem3d object is created as 
Fills a h2matrix with a predefined approximation technique.
This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix  is computed or a uniform rank-k-approximation specified within the bem3d object is created as
is computed or a uniform rank-k-approximation specified within the bem3d object is created as 
 and
and  have to be computed before calling this function because some approximation schemes depend on information residing within the clusterbasis.
have to be computed before calling this function because some approximation schemes depend on information residing within the clusterbasis.| void assemble_bem3d_h2matrix_col_clusterbasis | ( | pcbem3d | bem, |
| pclusterbasis | cb | ||
| ) |
This function computes the matrix entries for the nested clusterbasis  .
.
This algorithm completely traverses the clustertree belonging to the given clusterbasis until it reaches its leafs. In each leaf cluster the matrix  will be constructed and stored within the clusterbasis. In non leaf clusters the transfer matrices
will be constructed and stored within the clusterbasis. In non leaf clusters the transfer matrices  will be computed and it holds
will be computed and it holds
![\[ W_s = \begin{pmatrix} W_{s_1} & & \\ & \ddots & \\ & & W_{s_\sigma} \end{pmatrix} \begin{pmatrix} F_{s_1} \\ \vdots \\ F_{s_\sigma} \end{pmatrix} \]](../../form_228.png)
All matrices  will be stored within the clusterbasis belonging to the
will be stored within the clusterbasis belonging to the  -th son.
-th son.
| bem | bem3d object containing all necessary information for computing the entries of clusterbasis cb . |
| cb | Column clusterbasis to be filled. |
| void assemble_bem3d_h2matrix_row_clusterbasis | ( | pcbem3d | bem, |
| pclusterbasis | rb | ||
| ) |
This function computes the matrix entries for the nested clusterbasis  .
.
This algorithm completely traverses the clustertree belonging to the given clusterbasis until it reaches its leafs. In each leaf cluster the matrix  will be constructed and stored within the clusterbasis. In non leaf clusters the transfer matrices
will be constructed and stored within the clusterbasis. In non leaf clusters the transfer matrices  will be computed and it holds
will be computed and it holds
![\[ V_t = \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} \]](../../form_223.png)
All matrices  will be stored within the clusterbasis belonging to the
will be stored within the clusterbasis belonging to the  -th son.
-th son.
| bem | bem3d object containing all necessary information for computing the entries of clusterbasis rb . |
| rb | Row clusterbasis to be filled. |
Fills a hmatrix with a predefined approximation technique.
This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix  is computed or a rank-k-approximation specified within the bem3d object is created as
is computed or a rank-k-approximation specified within the bem3d object is created as 
| void assemble_bem3d_lagrange_amatrix | ( | const real(*) | X[3], |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will evaluate the Lagrange polynomials in a given point set X and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \mathcal L_\mu (\vec x_i) \]](../../form_236.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| X | An array of 3D-vectors. X[i][0] will be the first component of the i-th vector. Analogously X[i][1] will be the second component of the i-th vector. The length of this array is determined by V->cols . |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_lagrange_c_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu (\vec x) \, \mathrm d \vec x \]](../../form_231.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_lagrange_l_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu (\vec x) \, \mathrm d \vec x \]](../../form_231.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_lagrange_wave_amatrix | ( | const real(*) | X[3], |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcreal | dir, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will evaluate the modified Lagrange polynomials in a given point set X and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \mathcal L_{\mu, c} (\vec x_i) = \mathcal L_{\mu} (\vec x_i) \, e^{\langle c, \vec \vec x_i \rangle} \]](../../form_352.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| X | An array of 3D-vectors. X[i][0] will be the first component of the i-th vector. Analogously X[i][1] will be the second component of the i-th vector. The length of this array is determined by V->cols . |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| dir | Direction vector for the direction 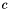 . . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_lagrange_wave_c_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcreal | dir, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate modified Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_{\mu, c} (\vec x) \, \mathrm d \vec x = \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_{\mu} (\vec x) \, e^{\langle c, \vec x \rangle} \, \mathrm d \vec x \]](../../form_349.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| dir | Direction vector for the direction 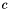 . . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_lagrange_wave_l_amatrix | ( | const uint * | idx, |
| pcrealavector | px, | ||
| pcrealavector | py, | ||
| pcrealavector | pz, | ||
| pcreal | dir, | ||
| pcbem3d | bem, | ||
| pamatrix | V | ||
| ) |
This function will integrate modified Lagrange polynomials on the boundary domain using linear basis function and store the results in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_{\mu, c} (\vec x) \, \mathrm d \vec x = \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_{\mu} (\vec x) \, e^{\langle c, \vec x \rangle} \, \mathrm d \vec x \]](../../form_349.png)
with Lagrange polynomial  defined as:
defined as:
![\[ \mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right) \cdot \left( \prod_{\nu_3 = 1, \nu_3 \neq \mu_3}^m \frac{\xi_{\nu_3} - x_3}{\xi_{\nu_3} - \xi_{\mu_3}} \right) \]](../../form_348.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| px | A Vector of type realavector that contains interpolation points in x-direction. |
| py | A Vector of type realavector that contains interpolation points in y-direction. |
| pz | A Vector of type realavector that contains interpolation points in z-direction. |
| dir | Direction vector for the direction 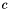 . . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| void assemble_bem3d_nearfield_dh2matrix | ( | pbem3d | bem, |
| pdh2matrix | G | ||
| ) |
Fills the nearfield blocks of a hmatrix.
This will traverse the block tree until it reaches its leafs. For an inadmissible leaf block the full matrix  is computed. In case of an admissible leaf no operations are performed.
is computed. In case of an admissible leaf no operations are performed.
| void assemble_cc_far_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise constant basis functions for both Ansatz and test functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_cc_near_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise constant basis functions for both Ansatz and test functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_cl_far_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise constant basis functions for Test and piecewise linear basis functions for Ansatz functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_cl_near_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise constant basis functions for Test and piecewise linear basis functions for Ansatz functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_lc_far_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise linear basis functions for Test and piecewise contant basis functions for Ansatz functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_lc_near_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise linear basis functions for Test and piecewise contant basis functions for Ansatz functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_ll_far_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise linear basis functions for both Ansatz and test functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
| void assemble_ll_near_bem3d | ( | const uint * | ridx, |
| const uint * | cidx, | ||
| pcbem3d | bem, | ||
| bool | ntrans, | ||
| pamatrix | N, | ||
| kernel_func3d | kernel | ||
| ) |
Compute general entries of a boundary integral operator with piecewise linear basis functions for both Ansatz and test functions.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| kernel | Defines the kernel function  to be used within the computation. to be used within the computation. |
Fills a hmatrix with a predefined approximation technique using coarsening strategy.
This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix  is computed or a rank-k-approximation specified within the bem3d object is created as
is computed or a rank-k-approximation specified within the bem3d object is created as  While traversing the block tree backwards coarsening algorithm determines whether current non leaf block could be stored more efficiently as a single compressed leaf block in rank-k-format or not.
While traversing the block tree backwards coarsening algorithm determines whether current non leaf block could be stored more efficiently as a single compressed leaf block in rank-k-format or not.
Fills an h2matrix with a predefined approximation technique using hierarchical recompression.
This functions does not need to initialized by an appropriate approximation technique for h2matrices. Instead one needs to specify a valid approximation scheme for hmatrices such as setup_hmatrix_aprx_inter_row_bem3d. When this method is finished not only the h2matrix G is filled but also the corresponding row and column clusterbasis.
 and
and  has to be allocated before calling this function.
has to be allocated before calling this function. For a block defined by row and col this function will compute the full submatrix and return an amatrix.
This function will simply create a new amatrix and call ((pcbem3d)data)->nearfield to compute the submatrix for this block.
| row | Row cluster defining the current hmatrix block. |
| col | Column cluster defining the current hmatrix block. |
| data | This object has to be a valid bem3d object. |
 .
. | pcluster build_bem3d_cluster | ( | pcbem3d | bem, |
| uint | clf, | ||
| basisfunctionbem3d | basis | ||
| ) |
Creates a clustertree for specified basis functions.
This function will build up a clustertree for a BEM-problem using basis functions of type basis. The maximal size of the leaves of the resulting tree are limited by clf. At first this function will call build_bem3d_clustergeometry and uses the temporary result to contruct a clustertree using build_adaptive_cluster.
| bem | At this stage bem just serves as a container for the geometry bem->gr itself. |
| clf | This parameter limits the maximals size of leafclusters. It holds:
|
| basis | This defines the type of basis functions that should be used to construct the cluster object. According to the type basisfunctionbem3d there are actual just to valid valued for basis: Either BASIS_CONSTANT_BEM3D or BASIS_LINEAR_BEM3D. |
| pclustergeometry build_bem3d_clustergeometry | ( | pcbem3d | bem, |
| uint ** | idx, | ||
| basisfunctionbem3d | basis | ||
| ) |
Creates a clustergeometry object for a BEM-Problem using the type of basis functions specified by basis.
The geometry is taken from the bem object as bem->gr .
| bem | At this stage bem just serves as a container for the geometry bem->gr itself. |
| idx | This method will allocate enough memory into idx to enumerate each degree of freedom. After calling build_bem3d_clustergeometry the value of idx will be 0, 1, ... N-1 if N is the number of degrees of freedom for basis functions defined by basis. |
| basis | This defines the type of basis functions that should be used to construct the clustergeometry object. According to the type basisfunctionbem3d there are actual just to valid valued for basis: Either BASIS_CONSTANT_BEM3D or BASIS_LINEAR_BEM3D. Depending on that value either build_bem3d_const_clustergeometry or build_bem3d_linear_clustergeometry will be called to build the object. |
| pclustergeometry build_bem3d_const_clustergeometry | ( | pcbem3d | bem, |
| uint ** | idx | ||
| ) |
Creates a clustergeometry object for a BEM-Problem using piecewise constant basis functions.
The geometry is taken from the bem object as bem->gr .
| bem | At this stage bem just serves as a container for the geometry bem->gr itself. |
| idx | This method will allocate enough memory into idx to enumerate each degree of freedom. After calling build_bem3d_const_clustergeometry the value of idx will be 0, 1, ... N-1 if N is the number of degrees of freedom for piecewise constant basis functions, which will be equal to the number of triangles in the geometry. |
| void build_bem3d_cube_quadpoints | ( | pcbem3d | bem, |
| const real | a[3], | ||
| const real | b[3], | ||
| const real | delta, | ||
| real(**) | Z[3], | ||
| real(**) | N[3] | ||
| ) |
Generating quadrature points, weights and normal vectors on a cube parameterization.
This function will build quadrature points, weight and appropriate outpointing normal vectors on a cube parameterization. The quadrature points are stored in parameter Z, for which storage will be allocated, the normal vectors and weights are stored within N and also storage will be allocated from this function.
| bem | BEM-object containing additional information for computation of the quadrature points, weight and normal vectors. |
| a | Minimal extent of the bounding box the parameterization will be constructed around. |
| b | Maximal extent of the bounding box the parameterization will be constructed around. |
| delta | Relative distance in terms of  the parameterization is afar from the bounding box the parameterization is afar from the bounding box  . . |
| Z | Resulting quadrature Points on the parameterization as array of 3D-vectors. Z[i][0] will be the first component of the i-th vector. Analogously Z[i][1] will be the second component of the i-th vector. The length of this array is defined within the function itself and the user has to know the length on his own. |
| N | Resulting quadrature weight and normal vectors on the parameterization as array of 3D-vectors. N[i][0] will be the first component of the i-th vector. Analogously N[i][1] will be the second component of the i-th vector. The length of this array is defined within the function itself and the user has to know the length on his own. Vectors do not have unit length instead it holds:
|
| void build_bem3d_curl_sparsematrix | ( | pcbem3d | bem, |
| psparsematrix * | C0, | ||
| psparsematrix * | C1, | ||
| psparsematrix * | C2 | ||
| ) |
Set up the surface curl operator.
This function creates three sparsematrix objects corresponding to the first, second, and third coordinates of the surface curl operator mapping linear nodal basis functions to piecewise constant basis functions.
| bem | BEM object. |
| C0 | First component, i.e.,  |
| C1 | Second component, i.e.,  |
| C2 | Third component, i.e.,  |
| pclustergeometry build_bem3d_linear_clustergeometry | ( | pcbem3d | bem, |
| uint ** | idx | ||
| ) |
Creates a clustergeometry object for a BEM-Problem using linear basis functions.
The geometry is taken from the bem object as bem->gr .
| bem | At this stage bem just serves as a container for the geometry bem->gr itself. |
| idx | This method will allocate enough memory into idx to enumerate each degree of freedom. After calling build_bem3d_linear_clustergeometry the value of idx will be 0, 1, ... N-1 if N is the number of degrees of freedom for linear basis functions, which will be equal to the number of vertices in the geometry. |
For a block defined by row and col this function will build a rank-k-approximation and return the rkmatrix.
This function will simply create a new rkmatrix and call ((pcbem3d)data)->farfield_rk to create the rank-k-approximation of this block.
| row | Row cluster defining the current hmatrix block. |
| col | Column cluster defining the current hmatrix block. |
| data | This object has to be a valid and initialized bem3d object. |
| void del_bem3d | ( | pbem3d | bem | ) |
| void del_tri_list | ( | ptri_list | tl | ) |
| void del_vert_list | ( | pvert_list | vl | ) |
| void fill_bem3d | ( | pcbem3d | bem, |
| const real(*) | X[3], | ||
| const real(*) | Y[3], | ||
| const real(*) | NX[3], | ||
| const real(*) | NY[3], | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
Evaluate a kernel function  at some points
at some points  and
and  .
.
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| X | An array of 3D-vectors. X[j][0] will be the first component of the j-th vector. Analogously X[j][1] will be the second component of the j-th vector. The length of this array is determined by V->rows . |
| Y | An array of 3D-vectors. Y[j][0] will be the first component of the j-th vector. Analogously Y[j][1] will be the second component of the j-th vector. The length of this array is determined by V->cols . |
| NX | An array of normal vectors corresponding to the vectors X. These are only needed |
| NY | An array of normal vectors corresponding to the vectors Y. |
| V | In the entry  the evaluation of the evaluation of  will be stored. will be stored. |
| kernel | A kernel function  that has to be evaluated at points that has to be evaluated at points  and and  . . |
| void fill_col_c_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a kernel function  on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points
on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \psi_i(\vec y) \, g(z_j, y) \, \mathrm d \vec y \]](../../form_333.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_col_l_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a kernel function  on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points
on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \psi_i(\vec y) \, g(z_j, y) \, \mathrm d \vec y \]](../../form_333.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_dnz_col_c_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| const real(*) | N[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a normal derivative of a kernel function  with respect to
with respect to  on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points
on the boundary domain in the second argument using piecewise constant basis function. For the first argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \psi_i(\vec y) \, \frac{\partial g}{\partial n_z}(z_j,y) \, \mathrm d \vec y \]](../../form_335.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| N | An array of normal vectors corresponding to the vectors Z. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_dnz_col_l_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| const real(*) | N[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a normal derivative of a kernel function  with respect to
with respect to  on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points
on the boundary domain in the second argument using piecewise linear basis function. For the first argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \psi_i(\vec y) \, \frac{\partial g}{\partial n_z}(z_j,y) \, \mathrm d \vec y \]](../../form_335.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| N | An array of normal vectors corresponding to the vectors Z. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_dnz_row_c_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| const real(*) | N[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a normal derivative of a kernel function  with respect to
with respect to 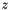 on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points
on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial g}{\partial n_z}(x, z_j) \, \mathrm d \vec x \]](../../form_334.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| N | An array of normal vectors corresponding to the vectors Z. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_dnz_row_l_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| const real(*) | N[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a normal derivative of a kernel function  with respect to
with respect to 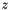 on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points
on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial g}{\partial n_z}(x, z_j) \, \mathrm d \vec x \]](../../form_334.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| N | An array of normal vectors corresponding to the vectors Z. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_row_c_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a kernel function  on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points
on the boundary domain in the first argument using piecewise constant basis function. For the second argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \varphi_i(\vec x) \, g(x, z_j) \, \mathrm d \vec x \]](../../form_332.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_row_l_bem3d | ( | const uint * | idx, |
| const real(*) | Z[3], | ||
| pcbem3d | bem, | ||
| pamatrix | V, | ||
| kernel_func3d | kernel | ||
| ) |
This function will integrate a kernel function  on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points
on the boundary domain in the first argument using piecewise linear basis function. For the second argument some given points  will be used. The results will be stored in a matrix
will be used. The results will be stored in a matrix V.
The matrix entries of V will be computed as
![\[ \left( V \right)_{ij} := \int_\Gamma \, \varphi_i(\vec x) \, g(x, z_j) \, \mathrm d \vec x \]](../../form_332.png)
| idx | This array describes the permutation of the degrees of freedom. Its length is determined by V->rows . In case idx == NULL it is assumed the degrees of freedom are  instead. instead. |
| Z | An array of 3D-vectors. Z[j][0] will be the first component of the j-th vector. Analogously Z[j][1] will be the second component of the j-th vector. The length of this array is determined by A->cols . |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| V | Matrix to store the computed results as stated above. |
| kernel | The kernel function to be integrated. |
| void fill_wave_bem3d | ( | pcbem3d | bem, |
| const real(*) | X[3], | ||
| const real(*) | Y[3], | ||
| const real(*) | NX[3], | ||
| const real(*) | NY[3], | ||
| pamatrix | V, | ||
| pcreal | dir, | ||
| kernel_wave_func3d | kernel | ||
| ) |
Evaluate a modified kernel function  at some points
at some points  and
and  for some direction
for some direction 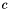 .
.
The function  can be decomposed as
can be decomposed as  .
.
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| X | An array of 3D-vectors. X[j][0] will be the first component of the j-th vector. Analogously X[j][1] will be the second component of the j-th vector. The length of this array is determined by V->rows . |
| Y | An array of 3D-vectors. Y[j][0] will be the first component of the j-th vector. Analogously Y[j][1] will be the second component of the j-th vector. The length of this array is determined by V->cols . |
| NX | An array of normal vectors corresponding to the vectors X. These are only needed |
| NY | An array of normal vectors corresponding to the vectors Y. |
| V | In the entry  the evaluation of the evaluation of  will be stored. will be stored. |
| dir | Direction  in which the modified kernel function should be evaluated. in which the modified kernel function should be evaluated. |
| kernel | A modified kernel function  that has to be evaluated at points that has to be evaluated at points  and and  . . |
| void integrate_bem3d_c_avector | ( | pbem3d | bem, |
| boundary_func3d | f, | ||
| pavector | w, | ||
| void * | data | ||
| ) |
Computes the integral of a given function using piecewise constant basis functions over the boundary of a domain.
The entries of the vector  are defined as:
are defined as:
![\[ f_i := \int_\Gamma \, \varphi_i(\vec x) \, r(\vec x, n(\vec x) ) \, \mathrm d \vec x \, , \]](../../form_361.png)
with  being the outpointing normal vector at the point
being the outpointing normal vector at the point  .
.
| bem | BEM-object containing additional information for computation of the vector entries. |
| f | This callback defines the function to be integrated. Its arguments are an evaluation 3D-vector x and its normal vector n. |
| w | The integration coefficients are stored within this vector. Therefore its length has to be at least bem->gr->triangles. |
| data | Additional data for evaluating the functional |
| void integrate_bem3d_l_avector | ( | pbem3d | bem, |
| boundary_func3d | f, | ||
| pavector | w, | ||
| void * | data | ||
| ) |
Computes the integral of a given function using piecewise linear basis functions over the boundary of a domain.
The entries of the vector  are defined as:
are defined as:
![\[ f_i := \int_\Gamma \, \varphi_i(\vec x) \, r(\vec x, n(\vec x) ) \, \mathrm d \vec x \, , \]](../../form_361.png)
with  being the outpointing normal vector at the point
being the outpointing normal vector at the point  .
.
| bem | BEM-object containing additional information for computation of the vector entries. |
| f | This callback defines the function to be integrated. Its arguments are an evaluation 3D-vector x and its normal vector n. |
| w | The integration coefficients are stored within this vector. Therefore its length has to be at least bem->gr->vertices. |
| data | Additional data for evaluating the functional |
| pbem3d new_bem3d | ( | pcsurface3d | gr, |
| basisfunctionbem3d | row_basis, | ||
| basisfunctionbem3d | col_basis | ||
| ) |
Main constructor for bem3d objects.
Primary constructor for bem3d objects. Although a valid bem3d object will be returned it is not intended to use this constructor. Instead use a problem specific constructor such as new_slp_laplace_bem3d or new_dlp_laplace_bem3d .
| gr | 3D geometry described as polyedric surface mesh. |
| row_basis | Type of basis functions that are used for the test space. Can be one of the values defined in basisfunctionbem3d. |
| col_basis | Type of basis functions that are used for the trial space. Can be one of the values defined in basisfunctionbem3d. |
Create a new list to store a number of triangles indices.
New list elements will be appended to the head of the list. Therefore the argument next has to point to the old list.
| next | Pointer to successor. |
next is returned. | pvert_list new_vert_list | ( | pvert_list | next | ) |
Create a new list to store a number of vertex indices.
New list elements will be appended to the head of the list. Therefore the argument next has to point to the old list.
| next | Pointer to successor. |
next is returned. | real normL2_bem3d | ( | pbem3d | bem, |
| boundary_func3d | f, | ||
| void * | data | ||
| ) |
Compute the  -norm of some given function
-norm of some given function f.
| bem | BEM-object containing additional information for the computation. |
| f | Function for that the norm should be computed. |
| data | Additional data needed to evaluate the function f. |
 is returned.
is returned. Compute the  -norm of some given function
-norm of some given function  in terms of a piecewise constant basis
in terms of a piecewise constant basis  .
.
It holds
![\[ f(\vec x) = \sum_{i \in \mathcal I} x_i \varphi_i(\vec x) \]](../../form_357.png)
| bem | BEM-object containing additional information for the computation. |
| x | Coefficient vector of  . . |
 is returned.
is returned. Compute the  -norm of some given function
-norm of some given function  in terms of a piecewise linear basis
in terms of a piecewise linear basis  .
.
It holds
![\[ f(\vec x) = \sum_{i \in \mathcal I} x_i \varphi_i(\vec x) \]](../../form_357.png)
| bem | BEM-object containing additional information for the computation. |
| x | Coefficient vector of  . . |
 is returned.
is returned. | real normL2diff_c_bem3d | ( | pbem3d | bem, |
| pavector | x, | ||
| boundary_func3d | f, | ||
| void * | data | ||
| ) |
Compute the  difference norm of some given function
difference norm of some given function  in terms of a piecewise constant basis
in terms of a piecewise constant basis  and some other function
and some other function  .
.
It holds
![\[ g(\vec x) = \sum_{i \in \mathcal I} x_i \varphi_i(\vec x) \]](../../form_358.png)
| bem | BEM-object containing additional information for the computation. |
| x | Coefficient vector of  . . |
| f | Function for that the norm should be computed. |
| data | Additional data needed to evaluate the function f. |
 is returned.
is returned. | real normL2diff_l_bem3d | ( | pbem3d | bem, |
| pavector | x, | ||
| boundary_func3d | f, | ||
| void * | data | ||
| ) |
Compute the  difference norm of some given function
difference norm of some given function  in terms of a piecewise linear basis
in terms of a piecewise linear basis  and some other function
and some other function  .
.
It holds
![\[ g(\vec x) = \sum_{i \in \mathcal I} x_i \varphi_i(\vec x) \]](../../form_358.png)
| bem | BEM-object containing additional information for the computation. |
| x | Coefficient vector of  . . |
| f | Function for that the norm should be computed. |
| data | Additional data needed to evaluate the function f. |
 is returned.
is returned. | void projectL2_bem3d_c_avector | ( | pbem3d | bem, |
| boundary_func3d | f, | ||
| pavector | w, | ||
| void * | data | ||
| ) |
Computes the  -projection of a given function using piecewise constant basis functions over the boundary of a domain.
-projection of a given function using piecewise constant basis functions over the boundary of a domain.
In case of piecewise constant basis functions the  -projection of a function
-projection of a function 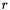 is defined as:
is defined as:
![\[ f_i := \frac{2}{\lvert \Gamma_i \rvert} \, \int_\Gamma \, \varphi_i(\vec x) \, r(\vec x, n(\vec x) ) \, \mathrm d \vec x \, , \]](../../form_362.png)
with  meaning the area of triangle
meaning the area of triangle  and
and  being the outpointing normal vector at the point
being the outpointing normal vector at the point  .
.
| bem | BEM-object containing additional information for computation of the vector entries. |
| f | This callback defines the function to be  projected. Its arguments are an evaluation 3D-vector projected. Its arguments are an evaluation 3D-vector x and its normal vector n. |
| w | The  -projection coefficients are stored within this vector. Therefore its length has to be at least -projection coefficients are stored within this vector. Therefore its length has to be at least bem->gr->triangles. |
| data | Additional data for evaluating the functional |
| void projectL2_bem3d_l_avector | ( | pbem3d | bem, |
| boundary_func3d | f, | ||
| pavector | w, | ||
| void * | data | ||
| ) |
Computes the  -projection of a given function using linear basis functions over the boundary of a domain.
-projection of a given function using linear basis functions over the boundary of a domain.
In case of linear basis functions the  -projection of a function
-projection of a function  is defined as:
is defined as:
![\[ v_i := \int_\Gamma \, \varphi_i(\vec x) \, r(\vec x, n(\vec x) ) \, \mathrm d \vec x \, , \]](../../form_363.png)
and then solving the equation
![\[ M \, f = v \]](../../form_364.png)
with  meaning the area of triangle
meaning the area of triangle  ,
,  being the outpointing normal vector at the point
being the outpointing normal vector at the point  and
and  being the mass matrix for linear basis functions defined as:
being the mass matrix for linear basis functions defined as:
![\[ M_{ij} := \int_\Gamma \varphi_i(\vec x) \, \varphi_j(\vec x) \, \mathrm d \vec x \, . \]](../../form_366.png)
| bem | BEM-object containing additional information for computation of the vector entries. |
| f | This callback defines the function to be  projected. Its arguments are an evaluation 3D-vector projected. Its arguments are an evaluation 3D-vector x and its normal vector n. |
| w | The  -projection coefficients are stored within this vector. Therefore its length has to be at least -projection coefficients are stored within this vector. Therefore its length has to be at least bem->gr->triangles. |
| data | Additional data for evaluating the functional |
| void setup_dh2matrix_aprx_inter_bem3d | ( | pbem3d | bem, |
| pcdclusterbasis | rb, | ||
| pcdclusterbasis | cb, | ||
| pcdblock | tree, | ||
| uint | m | ||
| ) |
Initialize the bem3d object for an interpolation based  -matrix approximation.
-matrix approximation.
All parameters and callback functions for a  -matrix approximation based on interpolation are set with this function and collected in the bem object.
-matrix approximation based on interpolation are set with this function and collected in the bem object.
| bem | Object filled with the needed parameters and callback functions for the approximation. |
| rb | dclusterbasis object for the row cluster. |
| cb | dclusterbasis object for the column cluster. |
| tree | Root of the block tree. |
| m | Number of interpolation points in each dimension. |
| void setup_dh2matrix_aprx_inter_ortho_bem3d | ( | pbem3d | bem, |
| pcdclusterbasis | rb, | ||
| pcdclusterbasis | cb, | ||
| pcdblock | tree, | ||
| uint | m | ||
| ) |
Initialize the bem3d object for an interpolation based  -matrix approximation with orthogonal directional cluster basis.
-matrix approximation with orthogonal directional cluster basis.
All parameters and callback functions for a  -matrix approximation based on interpolation and orthogonalized for smaller ranks are set with this function and collected in the bem object.
-matrix approximation based on interpolation and orthogonalized for smaller ranks are set with this function and collected in the bem object.
| bem | Object filled with the needed parameters and callback functions for the approximation. |
| rb | dclusterbasis object for the row cluster. |
| cb | dclusterbasis object for the column cluster. |
| tree | Root of the block tree. |
| m | Number of interpolation points in each dimension. |
| void setup_dh2matrix_aprx_inter_recomp_bem3d | ( | pbem3d | bem, |
| pcdclusterbasis | rb, | ||
| pcdclusterbasis | cb, | ||
| pcdblock | tree, | ||
| uint | m, | ||
| ptruncmode | tm, | ||
| real | eps | ||
| ) |
Initialize the bem3d object for an interpolation based  -matrix approximation with orthogonal directional cluster basis. During the filling process the
-matrix approximation with orthogonal directional cluster basis. During the filling process the  -matrix will be recompressed with respective to truncmode and the given accuracy
-matrix will be recompressed with respective to truncmode and the given accuracy eps.
All parameters and callback functions for a  -matrix approximation based on interpolation and immediate recompression for smaller ranks are set with this function and collected in the bem object.
-matrix approximation based on interpolation and immediate recompression for smaller ranks are set with this function and collected in the bem object.
| bem | Object filled with the needed parameters and callback functions for the approximation. |
| rb | dclusterbasis object for the row cluster. |
| cb | dclusterbasis object for the column cluster. |
| tree | Root of the block tree. |
| m | Number of interpolation points in each dimension. |
| tm | truncmode object for the choosen mode of truncation. |
| eps | desired accuracy for the truncation. |
| void setup_h2matrix_aprx_greenhybrid_bem3d | ( | pbem3d | bem, |
| pcclusterbasis | rb, | ||
| pcclusterbasis | cb, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| real | accur, | ||
| quadpoints3d | quadpoints | ||
| ) |
Initialize the bem3d object for approximating a h2matrix with green's method and ACA based recompression.
In case of leaf clusters, we use the techniques from setup_hmatrix_aprx_greenhybrid_row_bem3d and setup_hmatrix_aprx_greenhybrid_col_bem3d and construct two algebraic interpolation operators  and
and  and approximate an admissible block
and approximate an admissible block  by
by
![\[ G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* \, . \]](../../form_209.png)
This yields the representation:
![\[ G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* = V_t \, R_t \, G_{| t \times s} \, R_s^* \, W_s^* = V_t \, S_b \, W_s^* \]](../../form_210.png)
with  just a
just a  -matrix taking just the pivot rows and columns of the original matrix
-matrix taking just the pivot rows and columns of the original matrix  .
.
In case of non leaf clusters transfer matrices  and
and  are also introduced and the approximation of the block looks like:
are also introduced and the approximation of the block looks like:
![\[ G_{| t \times s} \approx \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \, \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} S_b \, \begin{pmatrix} F_{s_1}^* & \cdots & F_{s_\sigma}^* \end{pmatrix} \, \begin{pmatrix} W_{s_1}^* & & \\ & \ddots & \\ & & W_{s_\sigma}^* \end{pmatrix} \]](../../form_206.png)
The transfer matrices are build up in the following way: At first for a non leaf cluster  we construct a matrix
we construct a matrix  as in setup_hmatrix_aprx_green_row_bem3d but not with the index set
as in setup_hmatrix_aprx_green_row_bem3d but not with the index set  but with the index set
but with the index set
![\[ \bigcup_{t' \in \operatorname{sons}(t)} \, R_{t'} \, . \]](../../form_215.png)
Then again we use adaptive cross approximation technique to receive
![\[ A_t \approx C_t \, D_t^* \, . \]](../../form_216.png)
And again we construct an interpolation operator as before:
![\[ I_t := C_t \left( R_t \, C_t \right)^{-1} \, R_t \]](../../form_217.png)
And finally we have to solve
![\[ \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} = C_t \left( R_t \, C_t \right)^{-1} \]](../../form_218.png)
for our desired  .
.
Respectively the transfer matrices for the column clusterbasis are constructed.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rb | Root of the row clusterbasis. |
| cb | Root of the column clusterbasis. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  or or  and the Parameterization defined by quadpoints. and the Parameterization defined by quadpoints. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_h2matrix_aprx_greenhybrid_ortho_bem3d | ( | pbem3d | bem, |
| pcclusterbasis | rb, | ||
| pcclusterbasis | cb, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| real | accur, | ||
| quadpoints3d | quadpoints | ||
| ) |
Initialize the bem3d object for approximating a h2matrix with green's method and ACA based recompression. The resulting clusterbasis will be orthogonal.
In case of leaf clusters, we use the techniques similar to setup_hmatrix_aprx_greenhybrid_row_bem3d and setup_hmatrix_aprx_greenhybrid_col_bem3d and construct two algebraic interpolation operators  and
and  and approximate an admissible block
and approximate an admissible block  by
by
![\[ G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* \, . \]](../../form_209.png)
This yields the representation:
![\[ G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* = V_t \, R_t \, G_{| t \times s} \, R_s^* \, W_s^* = V_t \, S_b \, W_s^* \]](../../form_210.png)
with  just a
just a  -matrix taking just the pivot rows and columns of the original matrix
-matrix taking just the pivot rows and columns of the original matrix  .
.
In case of non leaf clusters transfer matrices  and
and  are also introduced and the approximation of the block looks like:
are also introduced and the approximation of the block looks like:
![\[ G_{| t \times s} \approx \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \, \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} S_b \, \begin{pmatrix} F_{s_1}^* & \cdots & F_{s_\sigma}^* \end{pmatrix} \, \begin{pmatrix} W_{s_1}^* & & \\ & \ddots & \\ & & W_{s_\sigma}^* \end{pmatrix} \]](../../form_206.png)
The transfer matrices are build up in the following way: At first for a non leaf cluster  we construct a matrix
we construct a matrix  as in setup_hmatrix_aprx_green_row_bem3d but not with the index set
as in setup_hmatrix_aprx_green_row_bem3d but not with the index set  but with the index set
but with the index set
![\[ \bigcup_{t' \in \operatorname{sons}(t)} \, R_{t'} \, . \]](../../form_215.png)
Then again we use adaptive cross approximation technique to receive
![\[ A_t \approx C_t \, D_t^* \, . \]](../../form_216.png)
And again we construct an interpolation operator as before:
![\[ I_t := C_t \left( R_t \, C_t \right)^{-1} \, R_t \]](../../form_217.png)
And finally we have to solve
![\[ \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} = C_t \left( R_t \, C_t \right)^{-1} \]](../../form_218.png)
for our desired  .
.
Respectively the transfer matrices for the column clusterbasis are constructed.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rb | Root of the row clusterbasis. |
| cb | Root of the column clusterbasis. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  or or  and the Parameterization defined by quadpoints. and the Parameterization defined by quadpoints. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_h2matrix_aprx_inter_bem3d | ( | pbem3d | bem, |
| pcclusterbasis | rb, | ||
| pcclusterbasis | cb, | ||
| pcblock | tree, | ||
| uint | m | ||
| ) |
Initialize the bem3d object for approximating a h2matrix with tensorinterpolation.
In case of leaf cluster  this approximation scheme creates a h2matrix approximation of the following form:
this approximation scheme creates a h2matrix approximation of the following form:
![\[ G_{| t \times s} \approx V_t \, S_b \, W_s^* \]](../../form_197.png)
with the matrices defined as
![\[ \left( V_t \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu(\vec x) \, \mathrm d \vec x \]](../../form_198.png)
![\[ \left( W_s \right)_{j\nu} := \int_\Gamma \, \Lambda_\nu(\vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \]](../../form_199.png)
![\[ \left( S_b \right)_{\mu\nu} := g(\vec \xi_\mu, \vec \xi_\nu) \, . \]](../../form_200.png)
Here  depends on the choice of the integral operator: in case of the single layer potential it applies
depends on the choice of the integral operator: in case of the single layer potential it applies  and in case of the double layer potential it applies
and in case of the double layer potential it applies  .
.
In case of non leaf clusters transfer matrices  and
and  are also constructed and the approximation of the block looks like:
are also constructed and the approximation of the block looks like:
![\[ G_{| t \times s} \approx \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \, \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} S_b \, \begin{pmatrix} F_{s_1}^* & \cdots & F_{s_\sigma}^* \end{pmatrix} \, \begin{pmatrix} W_{s_1}^* & & \\ & \ddots & \\ & & W_{s_\sigma}^* \end{pmatrix} \]](../../form_206.png)
The transfer matrices look like
![\[ \left( E_{t_i} \right)_{\mu\mu'} := \mathcal L_{\mu}(\xi_{\mu'}) \]](../../form_207.png)
respectively
![\[ \left( F_{s_j} \right)_{\nu\nu'} := \mathcal L_{\nu}(\xi_{\nu'}) \]](../../form_208.png)
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rb | Root of the row clusterbasis. |
| cb | Root of the column clusterbasis. |
| tree | Root of the blocktree. |
| m | Number of Chebyshev interpolation points in each spatial dimension. |
Enables hierarchical recompression for hmatrices.
This function enables hierarchical recompression. It is only necessary to initialize the bem3d object with some hmatrix compression technique such as setup_hmatrix_aprx_inter_row_bem3d . Afterwards one just has to call assemblehiercomp_bem3d_h2matrix to create a initially compressed h2matrix approximation.
| bem | All needed callback functions and parameters for h2-recompression are set within the bem object. |
| hiercomp | A flag to indicates whether hierarchical recompression should be used or not. |
| accur_hiercomp | The accuracy the hierarchical recompression technique will use to create a compressed h2matrix. |
| void setup_hmatrix_aprx_aca_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| real | accur | ||
| ) |
Approximate matrix block with ACA using full pivoting.
This approximation scheme will utilize adaptive cross approximation with full pivoting to retrieve a rank-k-approximation as
![\[ G_{|t \times s} \approx A_b \, B_b^* \]](../../form_181.png)
with a given accuracy accur.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| void setup_hmatrix_aprx_green_col_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| quadpoints3d | quadpoints | ||
| ) |
creating hmatrix approximation using green's method with column cluster .
This function initializes the bem3d object for approximating a matrix using green's formula. The approximation is based upon an expansion around the column cluster. For an admissible block  one yields an approximation in shape of
one yields an approximation in shape of
![\[ G_{|t \times s} \approx A_{t,s} \, B_s^* \quad \text{with} \]](../../form_135.png)
![\[ \left( A_{t,s}^1 \right)_{i\nu} := \omega_\nu \, \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial g}{\partial n_z} (\vec x, \vec z_\nu) \, \mathrm d \vec x \quad , \]](../../form_152.png)
![\[ \left( A_{t,s}^2 \right)_{i\nu} := \int_\Gamma \, \varphi_i(\vec x) \, g(\vec x, \vec z_\nu) \, \mathrm d \vec x \quad , \]](../../form_153.png)
![\[ A_{t,s} = \begin{pmatrix} A^1_{t,s} & A^2_{t,s} \end{pmatrix} \quad , \]](../../form_154.png)
![\[ \left( B_s^1 \right)_{j\nu} := \int_\Gamma \, \gamma (\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad , \]](../../form_155.png)
![\[ \left( B_s^2 \right)_{j\nu} := -\omega_\nu \, \int_\Gamma \, \frac{\partial \gamma}{\partial n_z}(\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad \text{and} \]](../../form_156.png)
![\[ B_s = \begin{pmatrix} B_s^1 & B_s^2 \end{pmatrix} . \]](../../form_157.png)
 is the underlying kernel function defined by the the integral operator. In case of single layer potential it applies
is the underlying kernel function defined by the the integral operator. In case of single layer potential it applies  but in case of double layer potential it applies
but in case of double layer potential it applies  . The green quadrature points
. The green quadrature points  and the weight
and the weight  depend on the choice of
depend on the choice of quadpoints and delta, which define the parameterization around the row cluster.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  and the Parameterization defined by quadpoints. and the Parameterization defined by quadpoints. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_hmatrix_aprx_green_mixed_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| quadpoints3d | quadpoints | ||
| ) |
creating hmatrix approximation using green's method with one of row or column cluster .
This function initializes the bem3d object for approximating a matrix using green's formula. The approximation is based upon an expansion around the row or column cluster depending on the diamter of their bounding boxes.. For an admissible block  one yields an approximation in shape of
one yields an approximation in shape of
![\[ G_{|t \times s} \approx \begin{cases} \begin{array}{ll} A_{t,s} \, B_s^* &: \operatorname{diam}(t) < \operatorname{diam}(s)\\ A_t \, B_{t,s}^* &: \operatorname{diam}(t) \geq \operatorname{diam}(s) \end{array} \end{cases} \]](../../form_159.png)
For definition of these matrices see setup_hmatrix_aprx_green_row_bem3d and setup_hmatrix_aprx_green_col_bem3d .
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  or or  and the Parameterization defined by quadpoints. and the Parameterization defined by quadpoints. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_hmatrix_aprx_green_row_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| quadpoints3d | quadpoints | ||
| ) |
creating hmatrix approximation using green's method with row cluster .
This function initializes the bem2d object for approximating a matrix using green's formula. The approximation is based upon an expansion around the row cluster. For an admissible block  one yields an approximation in shape of
one yields an approximation in shape of
![\[ G_{|t \times s} \approx A_t \, B_{t,s}^* \quad \text{with} \]](../../form_129.png)
![\[ \left( A_t^1 \right)_{i\nu} := \int_\Gamma \, \varphi_i(\vec x) \, g(\vec x, \vec z_\nu) \, \mathrm d \vec x \quad , \]](../../form_142.png)
![\[ \left( A_t^2 \right)_{i\nu} := \omega_\nu \, \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial g}{\partial n_z} (\vec x, \vec z_\nu) \, \mathrm d \vec x \quad , \]](../../form_143.png)
![\[ A_t = \begin{pmatrix} A^1_t & A^2_t \end{pmatrix} \quad , \]](../../form_144.png)
![\[ \left( B_{t,s}^1 \right)_{j\nu} := \omega_\nu \, \int_\Gamma \, \frac{\partial \gamma}{\partial n_z} (\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad , \]](../../form_145.png)
![\[ \left( B_{t,s}^2 \right)_{j\nu} := -\int_\Gamma \, \gamma(\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad \text{and} \]](../../form_146.png)
![\[ B_{t,s} = \begin{pmatrix} B_{t,s}^1 & B_{t,s}^2 \end{pmatrix} . \]](../../form_147.png)
 is the underlying kernel function defined by the the integral operator. In case of single layer potential it applies
is the underlying kernel function defined by the the integral operator. In case of single layer potential it applies  but in case of double layer potential it applies
but in case of double layer potential it applies  . The green quadrature points
. The green quadrature points  and the weight
and the weight  depend on the choice of
depend on the choice of quadpoints and delta, which define the parameterization around the row cluster.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  and the parameterization defined by quadpoints. and the parameterization defined by quadpoints. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_hmatrix_aprx_greenhybrid_col_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| real | accur, | ||
| quadpoints3d | quadpoints | ||
| ) |
creating hmatrix approximation using green's method with column cluster connected with recompression technique using ACA.
This function initializes the bem3d object for approximating a matrix using green's formula and ACA recompression. The approximation is based upon an expansion around the column cluster and a recompression using adaptive cross approximation.
In a first step the algorithm creates the same matrix  as in setup_hmatrix_aprx_green_col_bem3d. From this matrix we create a new approximation by using ACA with full pivoting (decomp_fullaca_rkmatrix) and we get a new rank-k-approximation of
as in setup_hmatrix_aprx_green_col_bem3d. From this matrix we create a new approximation by using ACA with full pivoting (decomp_fullaca_rkmatrix) and we get a new rank-k-approximation of  :
:
![\[ B_s \approx C_s \, D_s^* . \]](../../form_171.png)
Afterwards we define an algebraic interpolation operator
![\[ I_s := C_s \, \left(R_s \, C_s \right)^{-1} \, R_s \]](../../form_172.png)
with  selecting the pivot rows from the ACA-algorithm. Appling
selecting the pivot rows from the ACA-algorithm. Appling  to our matrix block
to our matrix block  we yield:
we yield:
![\[ G_{| t \times s} \approx G_{| t \times s} \, I_s^* = G_{| t \times s} \, \left( C_s \, \left(R_s \, C_s \right)^{-1} \, R_s \right)^* = A_{t,s} \, W_s^* \, . \]](../../form_175.png)
This defines our final approximation of the block with the matrices
![\[ A_{t,s} := G_{| t \times s} \, R_s^* \]](../../form_176.png)
and
![\[ W_s := C_s \, \left(R_s \, C_s \right)^{-1} \, . \]](../../form_177.png)
In order to save time and storage we compute the matrices  only once for each cluster
only once for each cluster  .
.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  and the parameterization defined by quadpoints. and the parameterization defined by quadpoints. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_hmatrix_aprx_greenhybrid_mixed_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| real | accur, | ||
| quadpoints3d | quadpoints | ||
| ) |
creating hmatrix approximation using green's method with row or column cluster connected with recompression technique using ACA.
This function initializes the bem3d object for approximating a matrix using green's formula and ACA recompression. The approximation is based upon an expansion around the row or column cluster and a recompression using adaptive cross approximation.
Depending on the rank produced by either setup_hmatrix_aprx_greenhybrid_row_bem3d or setup_hmatrix_aprx_greenhybrid_col_bem3d we define this approximation by
![\[ G_{|t \times s} \approx \begin{cases} \begin{array}{ll} V_t \, B_{t,s}* &: \operatorname{rank}(V_t) \leq \operatorname{rank}(W_s)\\ A_{t,s} \, W_s* &: \operatorname{rank}(V_t) > \operatorname{rank}(W_s) \quad . \end{array} \end{cases} \]](../../form_180.png)
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  or or  and the parameterization defined by quadpoints. and the parameterization defined by quadpoints. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_hmatrix_aprx_greenhybrid_row_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| uint | l, | ||
| real | delta, | ||
| real | accur, | ||
| quadpoints3d | quadpoints | ||
| ) |
creating hmatrix approximation using green's method with row cluster connected with recompression technique using ACA.
This function initializes the bem3d object for approximating a matrix using green's formula and ACA recompression. The approximation is based upon an expansion around the row cluster and a recompression using adaptive cross approximation.
In a first step the algorithm creates the same matrix  as in setup_hmatrix_aprx_green_row_bem3d. From this matrix we create a new approximation by using ACA with full pivoting (decomp_fullaca_rkmatrix) and we get a new rank-k-approximation of
as in setup_hmatrix_aprx_green_row_bem3d. From this matrix we create a new approximation by using ACA with full pivoting (decomp_fullaca_rkmatrix) and we get a new rank-k-approximation of  :
:
![\[ A_t \approx C_t \, D_t^* . \]](../../form_161.png)
Afterwards we define an algebraic interpolation operator
![\[ I_t := C_t \, \left(R_t \, C_t \right)^{-1} \, R_t \]](../../form_162.png)
with  selecting the pivot rows from the ACA-algorithm. Appling
selecting the pivot rows from the ACA-algorithm. Appling  to our matrix block
to our matrix block  we yield:
we yield:
![\[ G_{| t \times s} \approx I_t \, G_{| t \times s} = C_t \, \left(R_t \, C_t \right)^{-1} \, R_t \, G_{| t \times s} = V_t \, B_{t,s}^* \, . \]](../../form_166.png)
This defines our final approximation of the block with the matrices
![\[ V_t := C_t \, \left(R_t \, C_t \right)^{-1} \]](../../form_167.png)
and
![\[ B_{t,s} := \left( R_t \, G_{| t \times s} \right)^* \, . \]](../../form_168.png)
In order to save time and storage we compute the matrices  only once for each cluster
only once for each cluster  .
.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of gaussian quadrature points in each patch of the parameterization. |
| l | Number of subdivisions for gaussian quadrature in each patch of the parameterization. |
| delta | Defines the distance between the bounding box  and the parameterization defined by quadpoints. and the parameterization defined by quadpoints. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| quadpoints | This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization. |
| void setup_hmatrix_aprx_hca_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m, | ||
| real | accur | ||
| ) |
Approximate matrix block with hybrid cross approximation using Interpolation and ACA with full pivoting.
At first for a block  the matrix
the matrix  with
with  is set up with
is set up with  interpolation points from
interpolation points from  and
and  interpolation points from
interpolation points from  . Then applying ACA with full pivoting to
. Then applying ACA with full pivoting to  yields the representation:
yields the representation:
![\[ S_{\mu\nu} \approx \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \, S_{\mu \alpha} \, \hat S_{\alpha \beta} \, S_{\beta \nu} \]](../../form_186.png)
with  and
and  defining the pivot rows and columns from the ACA algoritm. This means we can rewrite the fundamental solution
defining the pivot rows and columns from the ACA algoritm. This means we can rewrite the fundamental solution  as follows:
as follows:
![\[ g(\vec x, \vec y) \approx \sum_{\mu = 1}^{m^3 }\sum_{\nu = 1}^{m^3} \mathcal L_\mu(\vec x) \, g(\vec \xi_\mu, \vec \xi\nu) \, \mathcal L_\nu(\vec y) \approx \sum_{\mu = 1}^{m^3 }\sum_{\nu = 1}^{m^3} \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \mathcal L_\mu(\vec x) \, S_{\mu \alpha} \, \hat S_{\alpha \beta} \, S_{\beta \nu} \, \mathcal L_\nu(\vec y) \]](../../form_336.png)
Now reversing the interpolation we can express this formula as:
![\[ g(\vec x, \vec y) \approx \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \, \hat S_{\alpha \beta} \, \sum_{\mu = 1}^{m^3 } \, \left( \mathcal L_\mu(\vec x) \, S_{\mu \alpha} \right) \, \sum_{\nu = 1}^{m^3} \left( S_{\beta \nu} \, \mathcal L_\nu(\vec y) \right) \approx \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \, g(\vec x, \vec \xi_\alpha) \, \hat S_{\alpha \beta} \, g(\vec \xi_\beta, \vec y) \]](../../form_337.png)
Depending on the condition  we can now construct the rank-k-approximation as
we can now construct the rank-k-approximation as
![\[ G_{|t \times s} \approx \left( A_b \, \hat S \right) \, B_b^* \quad \text{or} \]](../../form_192.png)
![\[ G_{|t \times s} \approx A_b \, \left( B_b \,\hat S \right)^* \]](../../form_193.png)
with matrices
![\[ \left( A_b \right)_{i\alpha} := \int_\Gamma \, \varphi(\vec x) \, g(\vec x, \vec \xi_\alpha) \, \mathrm d \vec x \quad , \]](../../form_194.png)
![\[ \left( B_b \right)_{j\beta} := \int_\Gamma \, g(\vec \xi_\beta, \vec y) \, \psi(\vec y) \, \mathrm d \vec y \quad . \]](../../form_195.png)
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of Chebyshev interpolation points in each spatial dimension. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| void setup_hmatrix_aprx_inter_col_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m | ||
| ) |
This function initializes the bem3d object for approximating a matrix with tensorinterpolation within the column cluster.
The approximation of an admissible block  is done by:
is done by:
![\[ G_{|t \times s} \approx A_{t,s} \, B_s^* \quad \text{with} \]](../../form_135.png)
![\[ \left( A_{t,s} \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, g(\vec x , \, \vec \xi_\mu) \, \mathrm d \vec x \quad \text{and} \]](../../form_136.png)
![\[ \left( B_s \right)_{j\mu} := \int_\Gamma \, \Lambda_\mu(\vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \, . \]](../../form_137.png)
with  being either the Lagrange polynomial
being either the Lagrange polynomial  itself in case of single layer potential, or
itself in case of single layer potential, or  in case of double layer potential.
in case of double layer potential.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of Chebyshev interpolation points in each spatial dimension. |
| void setup_hmatrix_aprx_inter_mixed_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m | ||
| ) |
This function initializes the bem3d object for approximating a matrix with tensorinterpolation within one of row or column cluster.
The interpolation depends on the condition:
![\[ G_{|t \times s} \approx \begin{cases}\begin{array}{ll} A_t \, B_{t,s}^* &: \operatorname{diam}(t) <\operatorname{diam}(s)\\ A_{t,s} \, B_s^* &: \operatorname{diam}(t) \geq \operatorname{diam}(s) \end{array} \end{cases} \]](../../form_141.png)
For definition of these matrices see setup_hmatrix_aprx_inter_row_bem3d and setup_hmatrix_aprx_inter_col_bem3d .
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of Chebyshev interpolation points in each spatial dimension. |
| void setup_hmatrix_aprx_inter_row_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| uint | m | ||
| ) |
This function initializes the bem3d object for approximating a matrix with tensorinterpolation within the row cluster.
The approximation of an admissible block  is done by:
is done by:
![\[ G_{|t \times s} \approx A_t \, B_{t,s}^* \quad \text{with} \]](../../form_129.png)
![\[ \left( A_t \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu(\vec x) \, \mathrm d \vec x \quad \text{and} \]](../../form_130.png)
![\[ \left( B_{t,s} \right)_{j\mu} := \int_\Gamma \, \gamma(\vec \xi_\mu , \, \vec y ) \, \psi_j(\vec y) \, \mathrm d \vec y \, . \]](../../form_131.png)
with  being the kernel function of the underlying integral operator. In case of the single layer potential this equal to the fundamental solution
being the kernel function of the underlying integral operator. In case of the single layer potential this equal to the fundamental solution  , in case of double layer potential this applies to
, in case of double layer potential this applies to  .
.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| m | Number of Chebyshev interpolation points in each spatial dimension. |
| void setup_hmatrix_aprx_paca_bem3d | ( | pbem3d | bem, |
| pccluster | rc, | ||
| pccluster | cc, | ||
| pcblock | tree, | ||
| real | accur | ||
| ) |
Approximate matrix block with ACA using partial pivoting.
This approximation scheme will utilize adaptive cross approximation with partial pivoting to retrieve a rank-k-approximation as
![\[ G_{|t \times s} \approx A_b \, B_b^* \]](../../form_181.png)
with a given accuracy accur.
| bem | All needed callback functions and parameters for this approximation scheme are set within the bem object. |
| rc | Root of the row clustertree. |
| cc | Root of the column clustertree. |
| tree | Root of the blocktree. |
| accur | Assesses the minimum accuracy for the ACA approximation. |
| void setup_hmatrix_recomp_bem3d | ( | pbem3d | bem, |
| bool | recomp, | ||
| real | accur_recomp, | ||
| bool | coarsen, | ||
| real | accur_coarsen | ||
| ) |
Initialize the bem object for on the fly recompression techniques.
| bem | According to the other parameters within bem->aprx there are set some flags that indicate which of the recompression techniques should be used while building up a hmatrix . |
| recomp | If this flag is set to true a blockwise recompression will be applied. For each block  independent on the approximation technique we will yield an approximation of the following kind: independent on the approximation technique we will yield an approximation of the following kind:
 depending on the accuracy accur_recomp depending on the accuracy accur_recomp |
| accur_recomp | The accuracy the blockwise recompression will used to compress a block with SVD. |
| coarsen | If a block consists of  sons which are all leafs of the blocktree, then it can be more efficient to store them as a single admissible leaf. This is done by "coarsening" recursively using the SVD. sons which are all leafs of the blocktree, then it can be more efficient to store them as a single admissible leaf. This is done by "coarsening" recursively using the SVD. |
| accur_coarsen | The accuracy the coarsen technique will use to determine the coarsened block structure. |
 1.8.11
1.8.11