This module contains main algorithms to solve boundary element method problems in 2 dimensional space. More...

Data Structures
struct	_bem2d
	Main container object for computation of BEM related matrices and vectors. More...

struct	_kernelbem2d
	Substructure containing callback functions to different types of kernel evaluations. More...

Typedefs
typedef struct _bem2d	bem2d

typedef bem2d *	pbem2d

typedef const bem2d *	pcbem2d

typedef struct _aprxbem2d	aprxbem2d

typedef aprxbem2d *	paprxbem2d

typedef const aprxbem2d *	pcaprxbem2d

typedef struct _parbem2d	parbem2d

typedef parbem2d *	pparbem2d

typedef const parbem2d *	pcparbem2d

typedef struct _kernelbem2d	kernelbem2d

typedef kernelbem2d *	pkernelbem2d

typedef const kernelbem2d *	pckernelbem2d

typedef void(*	quadpoints2d) (pcbem2d bem, const real bmin[2], const real bmax[2], const real delta, real(Z)[2], real(N)[2])
	Callback function type for parameterizations. More...

typedef enum _basisfunctionbem2d	basisfunctionbem2d

typedef field(*	boundary_func2d) (const real x, const real n)

Enumerations
enum	_basisfunctionbem2d { BASIS_NONE_BEM2D = 0, BASIS_CONSTANT_BEM2D = 'c', BASIS_LINEAR_BEM2D = 'l' }
	Possible types of basis functions. More...

Functions
pbem2d	new_bem2d (pccurve2d gr)
	Main constructor for bem2d objects. More...

void	del_bem2d (pbem2d bem)
	Destructor for bem2d objects. More...

pclustergeometry	build_bem2d_const_clustergeometry (pcbem2d bem, uint **idx)
	Creates a clustergeometry object for a BEM-Problem using piecewise constant basis functions. More...

pclustergeometry	build_bem2d_linear_clustergeometry (pcbem2d bem, uint **idx)
	Creates a clustergeometry object for a BEM-Problem using linear basis functions. More...

pclustergeometry	build_bem2d_clustergeometry (pcbem2d bem, uint **idx, basisfunctionbem2d basis)
	Creates a clustergeometry object for a BEM-Problem using the type of basis functions specified by basis. More...

pcluster	build_bem2d_cluster (pcbem2d bem, uint clf, basisfunctionbem2d basis)
	Creates a clustertree for specified basis functions. More...

void	setup_hmatrix_recomp_bem2d (pbem2d bem, bool recomp, real accur_recomp, bool coarsen, real accur_coarsen)
	Initialize the bem object for on the fly recompression techniques. More...

void	setup_hmatrix_aprx_inter_row_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m)
	This function initializes the bem2d object for approximating a matrix with tensorinterpolation within the row cluster. More...

void	setup_hmatrix_aprx_inter_col_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m)
	This function initializes the bem2d object for approximating a matrix with tensorinterpolation within the column cluster. More...

void	setup_hmatrix_aprx_inter_mixed_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m)
	This function initializes the bem2d object for approximating a matrix with tensorinterpolation within one of row or column cluster. More...

void	setup_hmatrix_aprx_green_row_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, quadpoints2d quadpoints)
	creating hmatrix approximation using green's method with row cluster . More...

void	setup_hmatrix_aprx_green_col_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, quadpoints2d quadpoints)
	creating hmatrix approximation using green's method with column cluster . More...

void	setup_hmatrix_aprx_green_mixed_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, quadpoints2d quadpoints)
	creating hmatrix approximation using green's method with one of row or column cluster . More...

void	setup_hmatrix_aprx_greenhybrid_row_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, real accur, quadpoints2d quadpoints)
	creating hmatrix approximation using green's method with row cluster connected with recompression technique using ACA. More...

void	setup_hmatrix_aprx_greenhybrid_col_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, real accur, quadpoints2d quadpoints)
	creating hmatrix approximation using green's method with column cluster connected with recompression technique using ACA. More...

void	setup_hmatrix_aprx_greenhybrid_mixed_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, uint l, real delta, real accur, quadpoints2d quadpoints)
	creating hmatrix approximation using green's method with row or column cluster connected with recompression technique using ACA. More...

void	setup_hmatrix_aprx_aca_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, real accur)
	Approximate matrix block with ACA using full pivoting. More...

void	setup_hmatrix_aprx_paca_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, real accur)
	Approximate matrix block with ACA using partial pivoting. More...

void	setup_hmatrix_aprx_hca_bem2d (pbem2d bem, pccluster rc, pccluster cc, pcblock tree, uint m, real accur)
	Approximate matrix block with hybrid cross approximation using Interpolation and ACA with full pivoting. More...

void	setup_h2matrix_recomp_bem2d (pbem2d bem, bool hiercomp, real accur_hiercomp)
	Enables hierarchical recompression for hmatrices. More...

void	setup_h2matrix_aprx_inter_bem2d (pbem2d bem, pcclusterbasis rb, pcclusterbasis cb, pcblock tree, uint m)
	Initialize the bem2d object for approximating a h2matrix with tensorinterpolation. More...

void	setup_h2matrix_aprx_greenhybrid_bem2d (pbem2d bem, pcclusterbasis rb, pcclusterbasis cb, pcblock tree, uint m, uint l, real delta, real accur, quadpoints2d quadpoints)
	Initialize the bem2d object for approximating a h2matrix with green's method and ACA based recompression. More...

void	setup_h2matrix_aprx_greenhybrid_ortho_bem2d (pbem2d bem, pcclusterbasis rb, pcclusterbasis cb, pcblock tree, uint m, uint l, real delta, real accur, quadpoints2d quadpoints)
	Initialize the bem2d object for approximating a h2matrix with green's method and ACA based recompression. The resulting clusterbasis will be orthogonal. More...

void	assemble_bem2d_hmatrix (pbem2d bem, pblock b, phmatrix G)
	Fills an hmatrix with a predefined approximation technique. More...

void	assemblecoarsen_bem2d_hmatrix (pbem2d bem, pblock b, phmatrix G)
	Fills an hmatrix with a predefined approximation technique using coarsening strategy. More...

void	assemble_bem2d_h2matrix_row_clusterbasis (pcbem2d bem, pclusterbasis rb)
	This function computes the matrix entries for the nested clusterbasis $V_t \, , t \in \mathcal T_{\mathcal I}$ . More...

void	assemble_bem2d_h2matrix_col_clusterbasis (pcbem2d bem, pclusterbasis cb)
	This function computes the matrix entries for the nested clusterbasis $W_s \, , s \in \mathcal T_{\mathcal J}$ . More...

void	assemble_bem2d_h2matrix (pbem2d bem, pblock b, ph2matrix G)
	Fills an h2matrix with a predefined approximation technique. More...

void	assemblehiercomp_bem2d_h2matrix (pbem2d bem, pblock b, ph2matrix G)
	Fills an h2matrix with a predefined approximation technique using hierarchical recompression. More...

void	assemble_bem2d_lagrange_const_amatrix (const uint *idx, pcavector px, pcavector py, pcbem2d bem, pamatrix V)
	This function will integrate Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix `V`. More...

void	assemble_bem2d_dn_lagrange_const_amatrix (const uint *idx, pcavector px, pcavector py, pcbem2d bem, pamatrix V)
	This function will integrate the normal derivatives of the Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix `V`. More...

void	assemble_bem2d_lagrange_amatrix (const real(*X)[2], pcavector px, pcavector py, pamatrix V)
	This function will evaluate the Lagrange polynomials in a given point set `X` and store the results in a matrix `V`. More...

void	projectl2_bem2d_const_avector (pbem2d bem, field(rhs)(const real x, const real *n), pavector f)
	Computes the -projection of a given function using piecewise constant basis functions. More...

void	build_bem2d_rect_quadpoints (pcbem2d bem, const real a[2], const real b[2], const real delta, real(Z)[2], real(N)[2])
	Generating quadrature points, weights and normal vectors on a rectangular parameterization. More...

void	build_bem2d_circle_quadpoints (pcbem2d bem, const real a[2], const real b[2], const real delta, real(Z)[2], real(N)[2])
	Generating quadrature points, weights and normal vectors on a circular parameterization. More...

prkmatrix	build_bem2d_rkmatrix (pccluster row, pccluster col, void *data)
	For a block defined by `row` and `col` this function will build a rank-k-approximation and return the rkmatrix. More...

pamatrix	build_bem2d_amatrix (pccluster row, pccluster col, void *data)
	For a block defined by `row` and `col` this function will compute the full submatrix and return an amatrix. More...

Detailed Description

This module contains main algorithms to solve boundary element method problems in 2 dimensional space.

bem2d provides basic functionality for a general BEM-application. Considering a special problem such as the Laplace-equation one has to include the laplacebem2d module, which provides the essential quadrature routines of the kernel functions. The bem2d module consists of a struct called bem2d, which contains a collection of callback functions, that regulates the whole computation of fully-populated BEM-matrices and also of h- and h2-matrices.

Typedef Documentation

typedef struct _aprxbem2d aprxbem2d

aprxbem2d is just an abbreviation for the struct _aprxbem2d hidden inside the bem2d.c file. This struct is necessary because of the different approximation techniques offered by this library. It will hide all dispensable information from the user.

typedef enum _basisfunctionbem2d basisfunctionbem2d

This is just an abbreviation for the enum _basisfunctionbem2d .

typedef struct _bem2d bem2d

bem2d is just an abbreviation for the struct _bem2d , which contains all necessary information to solve BEM-problems.

typedef field(* boundary_func2d) (const real *x, const real *n)

Defining a type for function that map from the boundary $\Gamma$ of the domain to a field $\mathbb K$ .

This type is used to define functions that produce example dirichlet and neumann data.

Parameters

x	2D-point the boundary $\Gamma$ .
n	Corresponding outpointing normal vector to `x`.

Returns: Returns evaluation of the function in x with normal vector n.

typedef struct _kernelbem2d kernelbem2d

kernelbem2d is just an abbreviation for the struct _kernelbem2d. It contains a collection of callback functions to evaluate or integrate kernel function and its derivatives.

typedef aprxbem2d* paprxbem2d

Pointer to a aprxbem2d object.

typedef struct _parbem2d parbem2d

parbem2d is just an abbreviation for the struct _parbem2d , which is hidden inside the bem2d.c . It is necessary for parallel computation on h- and and h2matrices.

typedef bem2d* pbem2d

Pointer to a bem2d object.

typedef const aprxbem2d* pcaprxbem2d

Pointer to a constant aprxbem2d object.

typedef const bem2d* pcbem2d

Pointer to a constant bem2d object.

typedef const kernelbem2d* pckernelbem2d

Pointer to a constant kernelbem2d object.

typedef const parbem2d* pcparbem2d

Pointer to a constant parbem2d object.

typedef kernelbem2d* pkernelbem2d

Pointer to a kernelbem2d object.

typedef parbem2d* pparbem2d

Pointer to a parbem2d object.

typedef void(* quadpoints2d) (pcbem2d bem, const real bmin[2], const real bmax[2], const real delta, real(**Z)[2], real(**N)[2])

Callback function type for parameterizations.

quadpoints2d defines a class of callback functions that are used to compute quadrature points, weight and normal vectors corresponding to the points on a given parameterization, which are used within the green's approximation functions. The parameters are in ascending order:

Parameters

bem	Reference to the bem2d object.
bmin	A 2D-array determining the minimal spatial dimensions of the bounding box the parameterization is located around.
bmax	A 2D-array determining the maximal spatial dimensions of the bounding box the parameterization is located around.
delta	Defines the distant between bounding box and the parameterization.
Z	The quadrature points will be stored inside of Z .
N	The outer normal vectors will be stored inside of N . For a quadrature point , a corresponding quadrature weight $\omega_i$ and the proper normal vector $\vec{n_i}$ the vector will not have unit length but $\lVert \vec{n_i} \rVert = \omega_i$ .

Enumeration Type Documentation

enum _basisfunctionbem2d

Possible types of basis functions.

This enum defines all possible values usable for basis functions for either neumann- and dirichlet-data. The values should be self-explanatory.

Attention: linear basis functions are not yet implemented.

Enumerator
BASIS_NONE_BEM2D	Dummy value, should never be used.
BASIS_CONSTANT_BEM2D	Enum value to represent piecewise constant basis functions.
BASIS_LINEAR_BEM2D	Enum value to represent piecewise linear basis functions.

Function Documentation

void assemble_bem2d_dn_lagrange_const_amatrix	(	const uint *	idx,
		pcavector	px,
		pcavector	py,
		pcbem2d	bem,
		pamatrix	V
	)

This function will integrate the normal derivatives of the Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V.

The matrix entries of V will be computed as

$\left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial \mathcal L_\mu}{\partial n} (\vec x) \, \mathrm d \vec x$

with Lagrange polynomial $\mathcal L_\mu (\vec x)$ defined as:

$\mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right)$

Parameters

idx	This array describes the permutation of the degrees of freedom. Its length is determined by `V->rows` . In case `idx == NULL` it is assumed the degrees of freedom are $0, 1, \ldots , \texttt{V->rows} -1$ instead.
px	A Vector of type avector that contains interpolation points in x-direction.
py	A Vector of type avector that contains interpolation points in y-direction.
bem	BEM-object containing additional information for computation of the matrix entries.
V	Matrix to store the computed results as stated above.

void assemble_bem2d_h2matrix	(	pbem2d	bem,
		pblock	b,
		ph2matrix	G
	)

Fills an h2matrix with a predefined approximation technique.

This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix $G_{|t \times s}$ is computed or a uniform rank-k-approximation specified within the bem2d object is created as $G_{|t \times s} \approx V_t \, S_b \, W_s^*$

Attention: Before using this function to fill an h2matrix one has to initialize the bem2d object with one of the approximation techniques such as setup_h2matrix_aprx_inter_bem2d. Otherwise the behavior of the function is undefined.; The clusterbasis and have to be computed before calling this function because some approximation schemes depend on information residing within the clusterbasis.

Parameters

bem	bem2d object containing all necessary information for computing the entries of h2matrix `G` .
b	Root of the blocktree.
G	h2matrix to be filled. `b` has to be appropriate to `G`.

void assemble_bem2d_h2matrix_col_clusterbasis	(	pcbem2d	bem,
		pclusterbasis	cb
	)

This function computes the matrix entries for the nested clusterbasis $W_s \, , s \in \mathcal T_{\mathcal J}$ .

This algorithm completely traverses the clustertree belonging to the given clusterbasis until it reaches its leafs. In each leaf cluster the matrix $ W_s $ will be constructed and stored within the clusterbasis. In non leaf clusters the transfer matrices $F_{s'} \, , s' \in \operatorname{sons}(s)$ will be computed and it holds

$W_s = \begin{pmatrix} W_{s_1} & & \\ & \ddots & \\ & & W_{s_\sigma} \end{pmatrix} \begin{pmatrix} F_{s_1} \\ \vdots \\ F_{s_\sigma} \end{pmatrix}$

A matrices $F_{s_i}$ will be stored within the clusterbasis belonging to the $ i $ -th son.

Attention: A valid h2matrix approximation scheme, such as setup_h2matrix_aprx_inter_bem2d must be set before calling this function. If no approximation technique is set within the bem2d object the behavior of this function is undefined.

Parameters

bem	bem2d object containing all necessary information for computing the entries of clusterbasis `rb` .
cb	Row clusterbasis to be filled.

void assemble_bem2d_h2matrix_row_clusterbasis	(	pcbem2d	bem,
		pclusterbasis	rb
	)

This function computes the matrix entries for the nested clusterbasis $V_t \, , t \in \mathcal T_{\mathcal I}$ .

This algorithm completely traverses the clustertree belonging to the given clusterbasis until it reaches its leafs. In each leaf cluster the matrix $ V_t $ will be constructed and stored within the clusterbasis. In non leaf clusters the transfer matrices $E_{t'} \, , t' \in \operatorname{sons}(t)$ will be computed and it holds

$V_t = \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix}$

A matrices $E_{t_i}$ will be stored within the clusterbasis belonging to the $ i $ -th son.

Attention: A valid h2matrix approximation scheme, such as setup_h2matrix_aprx_inter_bem2d must be set before calling this function. If no approximation technique is set within the bem2d object the behavior of this function is undefined.

Parameters

bem	bem2d object containing all necessary information for computing the entries of clusterbasis `rb` .
rb	Row clusterbasis to be filled.

void assemble_bem2d_hmatrix	(	pbem2d	bem,
		pblock	b,
		phmatrix	G
	)

Fills an hmatrix with a predefined approximation technique.

This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix $G_{|t \times s}$ is computed or a rank-k-approximation specified within the bem2d object is created as $G_{|t \times s} \approx A_b \, B_b^*$

Attention: Before using this function to fill an hmatrix one has to initialize the bem2d object with one of the approximation techniques such as setup_hmatrix_aprx_inter_row_bem2d. Otherwise the behavior of the function is undefined.

Parameters

bem	bem2d object containing all necessary information for computing the entries of hmatrix `G` .
b	Root of the blocktree.
G	hmatrix to be filled. `b` has to be appropriate to `G`.

void assemble_bem2d_lagrange_amatrix	(	const real(*)	X[2],
		pcavector	px,
		pcavector	py,
		pamatrix	V
	)

This function will evaluate the Lagrange polynomials in a given point set X and store the results in a matrix V.

The matrix entries of V will be computed as

$\left( V \right)_{i\mu} := \mathcal L_\mu (\vec x_i)$

with Lagrange polynomial $\mathcal L_\mu (\vec x)$ defined as:

$\mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right)$

Parameters

X	An array of 2D-vectors. `X[i][0]` will be the first component of the i-th vector. Analogously `X[i][1]` will be the second component of the i-th vector. The length of this array is determined by `V->cols` .
px	A Vector of type avector that contains interpolation points in x-direction.
py	A Vector of type avector that contains interpolation points in y-direction.
V	Matrix to store the computed results as stated above.

void assemble_bem2d_lagrange_const_amatrix	(	const uint *	idx,
		pcavector	px,
		pcavector	py,
		pcbem2d	bem,
		pamatrix	V
	)

This function will integrate Lagrange polynomials on the boundary domain using piecewise constant basis function and store the results in a matrix V.

The matrix entries of V will be computed as

$\left( V \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu (\vec x) \, \mathrm d \vec x$

with Lagrange polynomial $\mathcal L_\mu (\vec x)$ defined as:

$\mathcal L_\mu (\vec x) := \left( \prod_{\nu_1 = 1, \nu_1 \neq \mu_1}^m \frac{\xi_{\nu_1} - x_1}{\xi_{\nu_1} - \xi_{\mu_1}} \right) \cdot \left( \prod_{\nu_2 = 1, \nu_2 \neq \mu_2}^m \frac{\xi_{\nu_2} - x_2}{\xi_{\nu_2} - \xi_{\mu_2}} \right)$

Parameters

idx	This array describes the permutation of the degrees of freedom. Its length is determined by `V->rows` . In case `idx == NULL` it is assumed the degrees of freedom are $0, 1, \ldots , \texttt{V->rows} -1$ instead.
px	A Vector of type avector that contains interpolation points in x-direction.
py	A Vector of type avector that contains interpolation points in y-direction.
bem	BEM-object containing additional information for computation of the matrix entries.
V	Matrix to store the computed results as stated above.

void assemblecoarsen_bem2d_hmatrix	(	pbem2d	bem,
		pblock	b,
		phmatrix	G
	)

Fills an hmatrix with a predefined approximation technique using coarsening strategy.

This will traverse the block tree until it reaches its leafs. For a leaf block either the full matrix $G_{|t \times s}$ is computed or a rank-k-approximation specified within the bem2d object is created as $G_{|t \times s} \approx A_b \, B_b^*$ While traversing the block tree backwards coarsening algorithm determines whether current non leaf block could be stored more efficiently as a single compressed leaf block in rank-k-format or not.

Attention: Before using this function to fill an hmatrix one has to initialize the bem2d object with one of the approximation techniques such as setup_hmatrix_aprx_inter_row_bem2d. Otherwise the behavior of the function is undefined.; Make sure to call setup_hmatrix_recomp_bem2d with enabled coarsening and appropriate accuracy before calling this function. Default value of coarsening accuracy is set to 0.0, this means no coarsening will be done if a realistic accuracy is not set within the bem2d object.

Parameters

bem	bem2d object containing all necessary information for computing the entries of hmatrix `G` .
b	Root of the blocktree.
G	hmatrix to be filled. `b` has to be appropriate to `G`.

void assemblehiercomp_bem2d_h2matrix	(	pbem2d	bem,
		pblock	b,
		ph2matrix	G
	)

Fills an h2matrix with a predefined approximation technique using hierarchical recompression.

This functions does not need to initialized by an appropriate approximation technique for h2matrices. Instead one needs to specify a valid approximation scheme for hmatrices such as setup_hmatrix_aprx_inter_row_bem2d. When this method is finished not only the h2matrix G is filled but also the corresponding row and column clusterbasis.

Attention: Before using this function to fill an h2matrix one has to initialize the bem2d object with one of the hmatrix approximation techniques such as setup_hmatrix_aprx_inter_row_bem2d. Otherwise the behavior of the function is undefined.; Storage for the clusterbasis and has to be allocated before calling this function.; Before calling this function setup_h2matrix_recomp_bem2d has to be called enabling the hierarchical recompression with a valid accuracy. If this is not done, the default accuracy is set to 0.0. This will yield no reasonable approximation according to the resulting size of the h2matrix.

Parameters

bem	bem2d object containing all necessary information for computing the entries of h2matrix `G` .
b	Root of the blocktree.
G	h2matrix to be filled. `b` has to be appropriate to `G`.

pamatrix build_bem2d_amatrix	(	pccluster	row,
		pccluster	col,
		void *	data
	)

For a block defined by row and col this function will compute the full submatrix and return an amatrix.

This function will simply create a new amatrix and call ((pcbem2d)data)->nearfield to compute the submatrix for this block.

Parameters

row	Row cluster defining the current hmatrix block.
col	Column cluster defining the current hmatrix block.
data	This object has to be a valid bem2d object.

Returns: Submatrix $G_{|t \times s}$ .

void build_bem2d_circle_quadpoints	(	pcbem2d	bem,
		const real	a[2],
		const real	b[2],
		const real	delta,
		real(**)	Z[2],
		real(**)	N[2]
	)

Generating quadrature points, weights and normal vectors on a circular parameterization.

This function will build quadrature points, weight and appropriate outpointing normal vectors on a circular parameterization. The quadrature points are stored in parameter Z, for which storage will be allocated, the normal vectors and weights are stored within N and also storage will be allocated from this function.

Parameters

bem	BEM-object containing additional information for computation of the quadrature points, weight and normal vectors.
a	Minimal extent of the bounding box the parameterization will be constructed around.
b	Maximal extent of the bounding box the parameterization will be constructed around.
delta	Relative distance in terms of $\operatorname{diam}(B_t)$ the parameterization is afar from the bounding box .
Z	Resulting quadrature Points on the parameterization as array of 2D-vectors. `Z[i][0]` will be the first component of the i-th vector. Analogously `Z[i][1]` will be the second component of the i-th vector. The length of this array is defined within the function itself and the user has to know the length on his own.
N	Resulting quadrature weight and normal vectors on the parameterization as array of 2D-vectors. `N[i][0]` will be the first component of the i-th vector. Analogously `N[i][1]` will be the second component of the i-th vector. The length of this array is defined within the function itself and the user has to know the length on his own. Vectors do not have unit length instead it holds: $\lVert \vec n_i \rVert = \omega_i$

pcluster build_bem2d_cluster	(	pcbem2d	bem,
		uint	clf,
		basisfunctionbem2d	basis
	)

Creates a clustertree for specified basis functions.

This function will build up a clustertree for a BEM-problem using basis functions of type basis. The maximal size of the leaves of the resulting tree are limited by clf. At first this function will call build_bem2d_clustergeometry and uses the temporary result to contruct a clustertree using build_adaptive_cluster.

Parameters

bem	At this stage bem just serves as a container for the geometry `bem->gr` itself.
clf	This parameter limits the maximals size of leafclusters. It holds: $\# t \leq \texttt{clf} , \, \text{for all } t \in \mathcal L$
basis	This defines the type of basis functions that should be used to construct the cluster object. According to the type basisfunctionbem2d there are actual just to valid valued for basis: Either BASIS_CONSTANT_BEM2D or BASIS_LINEAR_BEM2D.

Returns: A suitable clustertree for basis functions defined by basis and using build_adaptive_cluster to build up the tree.

pclustergeometry build_bem2d_clustergeometry	(	pcbem2d	bem,
		uint **	idx,
		basisfunctionbem2d	basis
	)

Creates a clustergeometry object for a BEM-Problem using the type of basis functions specified by basis.

The geometry is taken from the bem object as bem->gr .

Parameters

bem	At this stage bem just serves as a container for the geometry `bem->gr` itself.
idx	This method will allocate enough memory into idx to enumerate each degree of freedom. After calling build_bem2d_clustergeometry the value of idx will be 0, 1, ... N-1 if N is the number of degrees of freedom for basis functions defined by basis.
basis	This defines the type of basis functions that should be used to construct the clustergeometry object. According to the type basisfunctionbem2d there are actual just to valid valued for basis: Either BASIS_CONSTANT_BEM2D or BASIS_LINEAR_BEM2D. Depending on that value either build_bem2d_const_clustergeometry or build_bem2d_linear_clustergeometry will be called to build the object.

Returns: Function will return a valid clustergeometry object that can be used to construct a clustertree along with the array of degrees of freedom idx.

pclustergeometry build_bem2d_const_clustergeometry	(	pcbem2d	bem,
		uint **	idx
	)

Creates a clustergeometry object for a BEM-Problem using piecewise constant basis functions.

The geometry is taken from the bem object as bem->gr .

Parameters

bem	At this stage bem just serves as a container for the geometry `bem->gr` itself.
idx	This method will allocate enough memory into idx to enumerate each degree of freedom. After calling build_bem2d_const_clustergeometry the value of idx will be 0, 1, ... N-1 if N is the number of degrees of freedom for piecewise constant basis functions, which will be equal to the number of edges in the geometry.

Returns: Function will return a valid clustergeometry object that can be used to construct a clustertree along with the array of degrees of freedom idx.

pclustergeometry build_bem2d_linear_clustergeometry	(	pcbem2d	bem,
		uint **	idx
	)

Creates a clustergeometry object for a BEM-Problem using linear basis functions.

The geometry is taken from the bem object as bem->gr .

Parameters

bem	At this stage bem just serves as a container for the geometry `bem->gr` itself.
idx	This method will allocate enough memory into idx to enumerate each degree of freedom. After calling build_bem2d_linear_clustergeometry the value of idx will be 0, 1, ... N-1 if N is the number of degrees of freedom for linear basis functions, which will be equal to the number of vertices in the geometry.

Attention: linear basis functions are not yet implemented.

Returns: Function will return a valid clustergeometry object that can be used to construct a clustertree along with the array of degrees of freedom idx.

void build_bem2d_rect_quadpoints	(	pcbem2d	bem,
		const real	a[2],
		const real	b[2],
		const real	delta,
		real(**)	Z[2],
		real(**)	N[2]
	)

Generating quadrature points, weights and normal vectors on a rectangular parameterization.

This function will build quadrature points, weight and appropriate outpointing normal vectors on a rectangular parameterization. The quadrature points are stored in parameter Z, for which storage will be allocated, the normal vectors and weights are stored within N and also storage will be allocated from this function.

Parameters

bem	BEM-object containing additional information for computation of the quadrature points, weight and normal vectors.
a	Minimal extent of the bounding box the parameterization will be constructed around.
b	Maximal extent of the bounding box the parameterization will be constructed around.
delta	Relative distance in terms of $\operatorname{diam}(B_t)$ the parameterization is afar from the bounding box .
Z	Resulting quadrature Points on the parameterization as array of 2D-vectors. `Z[i][0]` will be the first component of the i-th vector. Analogously `Z[i][1]` will be the second component of the i-th vector. The length of this array is defined within the function itself and the user has to know the length on his own.
N	Resulting quadrature weight and normal vectors on the parameterization as array of 2D-vectors. `N[i][0]` will be the first component of the i-th vector. Analogously `N[i][1]` will be the second component of the i-th vector. The length of this array is defined within the function itself and the user has to know the length on his own. Vectors do not have unit length instead it holds: $\lVert \vec n_i \rVert = \omega_i$

prkmatrix build_bem2d_rkmatrix	(	pccluster	row,
		pccluster	col,
		void *	data
	)

For a block defined by row and col this function will build a rank-k-approximation and return the rkmatrix.

This function will simply create a new rkmatrix and call ((pcbem2d)data)->farfield_rk to create the rank-k-approximation of this block.

Attention: Before calling this function take care of initializing the bem2d object with one the hmatrix approximation techniques such as setup_hmatrix_aprx_inter_row_bem2d. Not initialized bem2d object will cause undefined behavior.

Parameters

row	Row cluster defining the current hmatrix block.
col	Column cluster defining the current hmatrix block.
data	This object has to be a valid and initialized bem2d object.

Returns: A rank-k-approximation of the current block is returned.

void del_bem2d ( pbem2d bem )

Destructor for bem2d objects.

Delete a bem2d object.

Parameters

bem	bem2d object to be deleted.

pbem2d new_bem2d ( pccurve2d gr )

Main constructor for bem2d objects.

Primary constructor for bem2d objects. Although a valid bem2d object will be returned it is not intended to use this constructor. Instead use a problem specific constructor such as new_slp_laplace_bem2d or new_dlp_laplace_bem2d .

Parameters

gr	2D geometry described as polygonal mesh.

Returns: returns a valid bem2d object that will be used for almost all computations concerning a BEM-application.

void projectl2_bem2d_const_avector	(	pbem2d	bem,
		field()(const real x, const real *n)	rhs,
		pavector	f
	)

Computes the $ L_2 $ -projection of a given function using piecewise constant basis functions.

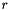In case of piecewise constant basis functions the $ L_2 $ -projection of a function $ r $ is defined as:

$f_i := \frac{1}{\lvert \Gamma_i \rvert} \, \int_\Gamma \, \varphi_i(\vec x) \, r(\vec x, n(\vec x) ) \, \mathrm d \vec x \, ,$

with $\lvert \Gamma_i \rvert$ meaning the area of triangle $ i $ and $n(\vec x)$ being the outpointing normal vector at the point $\vec x$ .

Parameters

bem	BEM-object containing additional information for computation of the vector entries.
rhs	This callback defines the function to be projected. Its arguments are an evaluation 2D-vector `x` and its normal vector `n`.
f	The -projection coefficients are stored within this vector. Therefore its length has to be at least `bem->gr->edges`.

void setup_h2matrix_aprx_greenhybrid_bem2d	(	pbem2d	bem,
		pcclusterbasis	rb,
		pcclusterbasis	cb,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		real	accur,
		quadpoints2d	quadpoints
	)

Initialize the bem2d object for approximating a h2matrix with green's method and ACA based recompression.

In case of lead clusters, we use the techniques from setup_hmatrix_aprx_greenhybrid_row_bem2d and setup_hmatrix_aprx_greenhybrid_col_bem2d and construct two algebraic interpolation operators $ I_t $ and $ I_s $ and approximate an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ by

$G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* \, .$

This yields the representation:

$G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* = V_t \, R_t \, G_{| t \times s} \, R_s^* \, W_s^* = V_t \, S_b \, W_s^*$

with $S_b := R_t \, G_{| t \times s} \, R_s^*$ just a $k \times k$ -matrix taking just the pivot rows and columns of the original matrix $G_{| t \times s}$ .

In case of non leaf clusters transfer matrices $E_{t_1} \ldots E_{t_\tau}$ and $F_{s_1} \ldots F_{s_\sigma}$ are also introduced and the approximation of the block looks like:

$G_{| t \times s} \approx \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \, \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} S_b \, \begin{pmatrix} F_{s_1}^* & \cdots & F_{s_\sigma}^* \end{pmatrix} \, \begin{pmatrix} W_{s_1}^* & & \\ & \ddots & \\ & & W_{s_\sigma}^* \end{pmatrix}$

The transfer matrices are build up in the following way: At first for a non leaf cluster $t \in \mathcal T_{\mathcal I}$ we construct a matrix $ A_t $ as in setup_hmatrix_aprx_green_row_bem2d but not with the index set $\hat t$ but with the index set

$\bigcup_{t' \in \operatorname{sons}(t)} \, R_{t'} \, .$

Then again we use adaptive cross approximation technique to receive

$A_t \approx C_t \, D_t^* \, .$

And again we construct an interpolation operator as before:

$I_t := C_t \left( R_t \, C_t \right)^{-1} \, R_t$

And finally we have to solve

$\begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} = C_t \left( R_t \, C_t \right)^{-1}$

for our desired $E_{t'}$ .
Respectively the transfer matrices for the column clusterbasis are constructed.

See also: setup_hmatrix_aprx_greenhybrid_row_bem2d; setup_hmatrix_aprx_greenhybrid_col_bem2d

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rb	Root of the row clusterbasis.
cb	Root of the column clusterbasis.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box or and the Parameterization defined by quadpoints.
accur	Assesses the minimum accuracy for the ACA approximation.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_h2matrix_aprx_greenhybrid_ortho_bem2d	(	pbem2d	bem,
		pcclusterbasis	rb,
		pcclusterbasis	cb,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		real	accur,
		quadpoints2d	quadpoints
	)

Initialize the bem2d object for approximating a h2matrix with green's method and ACA based recompression. The resulting clusterbasis will be orthogonal.

In case of leaf clusters, we use the techniques similar to setup_hmatrix_aprx_greenhybrid_row_bem2d and setup_hmatrix_aprx_greenhybrid_col_bem2d and construct two algebraic interpolation operators $ I_t $ and $ I_s $ and approximate an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ by

$G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* \, .$

This yields the representation:

$G_{| t \times s} \approx I_t \, G_{| t \times s} \, I_s^* = V_t \, R_t \, G_{| t \times s} \, R_s^* \, W_s^* = V_t \, S_b \, W_s^*$

with $S_b := R_t \, G_{| t \times s} \, R_s^*$ just a $k \times k$ -matrix taking just the pivot rows and columns of the original matrix $G_{| t \times s}$ .

In case of non leaf clusters transfer matrices $E_{t_1} \ldots E_{t_\tau}$ and $F_{s_1} \ldots F_{s_\sigma}$ are also introduced and the approximation of the block looks like:

$G_{| t \times s} \approx \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \, \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} S_b \, \begin{pmatrix} F_{s_1}^* & \cdots & F_{s_\sigma}^* \end{pmatrix} \, \begin{pmatrix} W_{s_1}^* & & \\ & \ddots & \\ & & W_{s_\sigma}^* \end{pmatrix}$

The transfer matrices are build up in the following way: At first for a non leaf cluster $t \in \mathcal T_{\mathcal I}$ we construct a matrix $ A_t $ as in setup_hmatrix_aprx_green_row_bem2d but not with the index set $\hat t$ but with the index set

$\bigcup_{t' \in \operatorname{sons}(t)} \, R_{t'} \, .$

Then again we use adaptive cross approximation technique to receive

$A_t \approx C_t \, D_t^* \, .$

And again we construct an interpolation operator as before:

$I_t := C_t \left( R_t \, C_t \right)^{-1} \, R_t$

And finally we have to solve

$\begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} = C_t \left( R_t \, C_t \right)^{-1}$

for our desired $E_{t'}$ .
Respectively the transfer matrices for the column clusterbasis are constructed.

See also: setup_hmatrix_aprx_greenhybrid_row_bem2d; setup_hmatrix_aprx_greenhybrid_col_bem2d

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rb	Root of the row clusterbasis.
cb	Root of the column clusterbasis.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box or and the Parameterization defined by quadpoints.
accur	Assesses the minimum accuracy for the ACA approximation.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_h2matrix_aprx_inter_bem2d	(	pbem2d	bem,
		pcclusterbasis	rb,
		pcclusterbasis	cb,
		pcblock	tree,
		uint	m
	)

Initialize the bem2d object for approximating a h2matrix with tensorinterpolation.

In case of leaf cluster $ t, s $ this approximation scheme creates a h2matrix approximation of the following form:

$G_{| t \times s} \approx V_t \, S_b \, W_s^*$

with the matrices defined as

$\left( V_t \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu(\vec x) \, \mathrm d \vec x$

$\left( W_s \right)_{j\nu} := \int_\Gamma \, \Lambda_\nu(\vec y) \, \psi_j(\vec y) \, \mathrm d \vec y$

$\left( S_b \right)_{\mu\nu} := g(\vec \xi_\mu, \vec \xi_\nu) \, .$

Here $\Lambda_\nu$ depends on the choice of the integral operator: in case of the single layer potential it applies $\Lambda_\nu = \mathcal L_\nu$ and in case of the double layer potential it applies $\Lambda_\nu = \frac{\partial \mathcal L_\nu}{\partial n}$ .

In case of non leaf clusters transfer matrices $E_{t_1} \ldots E_{t_\tau}$ and $F_{s_1} \ldots F_{s_\sigma}$ are also constructed and the approximation of the block looks like:

$G_{| t \times s} \approx \begin{pmatrix} V_{t_1} & & \\ & \ddots & \\ & & V_{t_\tau} \end{pmatrix} \, \begin{pmatrix} E_{t_1} \\ \vdots \\ E_{t_\tau} \end{pmatrix} S_b \, \begin{pmatrix} F_{s_1}^* & \cdots & F_{s_\sigma}^* \end{pmatrix} \, \begin{pmatrix} W_{s_1}^* & & \\ & \ddots & \\ & & W_{s_\sigma}^* \end{pmatrix}$

The transfer matrices look like

$\left( E_{t_i} \right)_{\mu\mu'} := \mathcal L_{\mu}(\xi_{\mu'})$

respectively

$\left( F_{s_j} \right)_{\nu\nu'} := \mathcal L_{\nu}(\xi_{\nu'})$

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rb	Root of the row clusterbasis.
cb	Root of the column clusterbasis.
tree	Root of the blocktree.
m	Number of Chebyshev interpolation points in each spatial dimension.

void setup_h2matrix_recomp_bem2d	(	pbem2d	bem,
		bool	hiercomp,
		real	accur_hiercomp
	)

Enables hierarchical recompression for hmatrices.

This function enables hierarchical recompression. It is only necessary to initialize the bem2d object with some hmatrix compression technique such as setup_hmatrix_aprx_inter_row_bem2d . Afterwards one just has to call assemblehiercomp_bem2d_h2matrix to create a initially compressed h2matrix approximation.

Parameters

bem	All needed callback functions and parameters for h2-recompression are set within the bem object.
hiercomp	A flag to indicates whether hierarchical recompression should be used or not.
accur_hiercomp	The accuracy the hierarchical recompression technique will use to create a compressed h2matrix.

void setup_hmatrix_aprx_aca_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		real	accur
	)

Approximate matrix block with ACA using full pivoting.

This approximation scheme will utilize adaptive cross approximation with full pivoting to retrieve a rank-k-approximation as

$G_{|t \times s} \approx A_b \, B_b^*$

with a given accuracy accur.

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
accur	Assesses the minimum accuracy for the ACA approximation.

void setup_hmatrix_aprx_green_col_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		quadpoints2d	quadpoints
	)

creating hmatrix approximation using green's method with column cluster .

This function initializes the bem2d object for approximating a matrix using green's formula. The approximation is based upon an expansion around the column cluster. For an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ one yields an approximation in shape of

$G_{|t \times s} \approx A_{t,s} \, B_s^* \quad \text{with}$

$\left( A_{t,s}^1 \right)_{i\nu} := \omega_\nu \, \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial g}{\partial n_z} (\vec x, \vec z_\nu) \, \mathrm d \vec x \quad ,$

$\left( A_{t,s}^2 \right)_{i\nu} := \int_\Gamma \, \varphi_i(\vec x) \, g(\vec x, \vec z_\nu) \, \mathrm d \vec x \quad ,$

$A_{t,s} = \begin{pmatrix} A^1_{t,s} & A^2_{t,s} \end{pmatrix} \quad ,$

$\left( B_s^1 \right)_{j\nu} := \int_\Gamma \, \gamma (\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad ,$

$\left( B_s^2 \right)_{j\nu} := -\omega_\nu \, \int_\Gamma \, \frac{\partial \gamma}{\partial n_z}(\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad \text{and}$

$B_s = \begin{pmatrix} B_s^1 & B_s^2 \end{pmatrix} .$

$\gamma$ is the underlying kernel function defined by the the integral operator. In case of single layer potential it applies $\gamma = g$ but in case of double layer potential it applies $\gamma = \frac{\partial g}{\partial n_y}$ . The green quadrature points $z_\nu$ and the weight $\omega_\nu$ depend on the choice of quadpoints and delta, which define the parameterization around the row cluster.

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box and the Parameterization defined by quadpoints.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_hmatrix_aprx_green_mixed_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		quadpoints2d	quadpoints
	)

creating hmatrix approximation using green's method with one of row or column cluster .

This function initializes the bem2d object for approximating a matrix using green's formula. The approximation is based upon an expansion around the row or column cluster depending on the diamter of their bounding boxes.. For an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ one yields an approximation in shape of

$G_{|t \times s} \approx \begin{cases} \begin{array}{ll} A_{t,s} \, B_s^* &: \operatorname{diam}(t) < \operatorname{diam}(s)\\ A_t \, B_{t,s}^* &: \operatorname{diam}(t) \geq \operatorname{diam}(s) \end{array} \end{cases}$

For definition of these matrices see setup_hmatrix_aprx_green_row_bem2d and setup_hmatrix_aprx_green_col_bem2d .

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box or and the Parameterization defined by quadpoints.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_hmatrix_aprx_green_row_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		quadpoints2d	quadpoints
	)

creating hmatrix approximation using green's method with row cluster .

This function initializes the bem2d object for approximating a matrix using green's formula. The approximation is based upon an expansion around the row cluster. For an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ one yields an approximation in shape of

$G_{|t \times s} \approx A_t \, B_{t,s}^* \quad \text{with}$

$\left( A_t^1 \right)_{i\nu} := \int_\Gamma \, \varphi_i(\vec x) \, g(\vec x, \vec z_\nu) \, \mathrm d \vec x \quad ,$

$\left( A_t^2 \right)_{i\nu} := \omega_\nu \, \int_\Gamma \, \varphi_i(\vec x) \, \frac{\partial g}{\partial n_z} (\vec x, \vec z_\nu) \, \mathrm d \vec x \quad ,$

$A_t = \begin{pmatrix} A^1_t & A^2_t \end{pmatrix} \quad ,$

$\left( B_{t,s}^1 \right)_{j\nu} := \omega_\nu \, \int_\Gamma \, \frac{\partial \gamma}{\partial n_z} (\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad ,$

$\left( B_{t,s}^2 \right)_{j\nu} := -\int_\Gamma \, \gamma(\vec z_\nu, \vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \quad \text{and}$

$B_{t,s} = \begin{pmatrix} B_{t,s}^1 & B_{t,s}^2 \end{pmatrix} .$

$\gamma$ is the underlying kernel function defined by the the integral operator. In case of single layer potential it applies $\gamma = g$ but in case of double layer potential it applies $\gamma = \frac{\partial g}{\partial n_y}$ . The green quadrature points $z_\nu$ and the weight $\omega_\nu$ depend on the choice of quadpoints and delta, which define the parameterization around the row cluster.

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box and the parameterization defined by quadpoints.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_hmatrix_aprx_greenhybrid_col_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		real	accur,
		quadpoints2d	quadpoints
	)

creating hmatrix approximation using green's method with column cluster connected with recompression technique using ACA.

This function initializes the bem2d object for approximating a matrix using green's formula and ACA recompression. The approximation is based upon an expansion around the column cluster and a recompression using adaptive cross approximation.

In a first step the algorithm creates the same matrix $ B_s $ as in setup_hmatrix_aprx_green_col_bem2d. From this matrix we create a new approximation by using ACA with full pivoting (decomp_fullaca_rkmatrix) and we get a new rank-k-approximation of $ B_s $ :

$B_s \approx C_s \, D_s^* .$

Afterwards we define an algebraic interpolation operator

$I_s := C_s \, \left(R_s \, C_s \right)^{-1} \, R_s$

with $ R_s $ selecting the pivot rows from the ACA-algorithm. Appling $ I_s $ to our matrix block $G_{|t \times s}$ we yield:

$G_{| t \times s} \approx G_{| t \times s} \, I_s^* = G_{| t \times s} \, \left( C_s \, \left(R_s \, C_s \right)^{-1} \, R_s \right)^* = A_{t,s} \, W_s^* \, .$

This defines our final approximation of the block with the matrices

$A_{t,s} := G_{| t \times s} \, R_s^*$

and

$W_s := C_s \, \left(R_s \, C_s \right)^{-1} \, .$

In order to save time and storage we compute the matrices $ W_s $ only once for each cluster $s \in \mathcal T_{\mathcal J}$ .

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box and the parameterization defined by quadpoints.
accur	Assesses the minimum accuracy for the ACA approximation.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_hmatrix_aprx_greenhybrid_mixed_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		real	accur,
		quadpoints2d	quadpoints
	)

creating hmatrix approximation using green's method with row or column cluster connected with recompression technique using ACA.

This function initializes the bem2d object for approximating a matrix using green's formula and ACA recompression. The approximation is based upon an expansion around the row or column cluster and a recompression using adaptive cross approximation.

Depending on the rank produced by either setup_hmatrix_aprx_greenhybrid_row_bem2d or setup_hmatrix_aprx_greenhybrid_col_bem2d we define this approximation by

$G_{|t \times s} \approx \begin{cases} \begin{array}{ll} V_t \, B_{t,s}* &: \operatorname{rank}(V_t) \leq \operatorname{rank}(W_s)\\ A_{t,s} \, W_s* &: \operatorname{rank}(V_t) > \operatorname{rank}(W_s) \quad . \end{array} \end{cases}$

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box or and the parameterization defined by quadpoints.
accur	Assesses the minimum accuracy for the ACA approximation.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_hmatrix_aprx_greenhybrid_row_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		uint	l,
		real	delta,
		real	accur,
		quadpoints2d	quadpoints
	)

creating hmatrix approximation using green's method with row cluster connected with recompression technique using ACA.

This function initializes the bem2d object for approximating a matrix using green's formula and ACA recompression. The approximation is based upon an expansion around the row cluster and a recompression using adaptive cross approximation.

In a first step the algorithm creates the same matrix $ A_t $ as in setup_hmatrix_aprx_green_row_bem2d. From this matrix we create a new approximation by using ACA with full pivoting (decomp_fullaca_rkmatrix) and we get a new rank-k-approximation of $ A_t $ :

$A_t \approx C_t \, D_t^* .$

Afterwards we define an algebraic interpolation operator

$I_t := C_t \, \left(R_t \, C_t \right)^{-1} \, R_t$

with $ R_t $ selecting the pivot rows from the ACA-algorithm. Appling $ I_t $ to our matrix block $G_{|t \times s}$ we yield:

$G_{| t \times s} \approx I_t \, G_{| t \times s} = C_t \, \left(R_t \, C_t \right)^{-1} \, R_t \, G_{| t \times s} = V_t \, B_{t,s}^* \, .$

This defines our final approximation of the block with the matrices

$V_t := C_t \, \left(R_t \, C_t \right)^{-1}$

and

$B_{t,s} := \left( R_t \, G_{| t \times s} \right)^* \, .$

In order to save time and storage we compute the matrices $ V_t $ only once for each cluster $t \in \mathcal T_{\mathcal I}$ .

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of gaussian quadrature points in each patch of the parameterization.
l	Number of subdivisions for gaussian quadrature in each patch of the parameterization.
delta	Defines the distance between the bounding box and the parameterization defined by quadpoints.
accur	Assesses the minimum accuracy for the ACA approximation.
quadpoints	This callback function defines a parameterization and it has to return valid quadrature points, weight and normalvectors on the parameterization.

void setup_hmatrix_aprx_hca_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m,
		real	accur
	)

Approximate matrix block with hybrid cross approximation using Interpolation and ACA with full pivoting.

At first for a block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ the matrix $ S $ with $S_{\mu\nu} = g(\vec \xi_\mu, \vec \xi\nu)$ is set up with $\vec \xi_\mu$ interpolation points from $ B_t $ and $\vec \xi_\nu$ interpolation points from $ B_s $ . Then applying ACA with full pivoting to $ S $ yields the representation:

$S_{\mu\nu} \approx \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \, S_{\mu \alpha} \, \hat S_{\alpha \beta} \, S_{\beta \nu}$

with $\hat S := \left( S_{|I_t \times I_s} \right)^{-1}$ and $I_t \, , I_s$ defining the pivot rows and columns from the ACA algoritm. This means we can rewrite the fundamental solution $ g $ as follows:

$g(\vec x, \vec y) \approx \sum_{\mu = 1}^{m^2 }\sum_{\nu = 1}^{m^2} \mathcal L_\mu(\vec x) \, g(\vec \xi_\mu, \vec \xi\nu) \, \mathcal L_\nu(\vec y) \approx \sum_{\mu = 1}^{m^2 }\sum_{\nu = 1}^{m^2} \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \mathcal L_\mu(\vec x) \, S_{\mu \alpha} \, \hat S_{\alpha \beta} \, S_{\beta \nu} \, \mathcal L_\nu(\vec y)$

Now reversing the interpolation we can express this formula as:

$g(\vec x, \vec y) \approx \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \, \hat S_{\alpha \beta} \, \sum_{\mu = 1}^{m^2 } \, \left( \mathcal L_\mu(\vec x) \, S_{\mu \alpha} \right) \, \sum_{\nu = 1}^{m^2} \left( S_{\beta \nu} \, \mathcal L_\nu(\vec y) \right) \approx \sum_{\alpha = 1}^k \sum_{\beta = 1}^k \, g(\vec x, \vec \xi_\alpha) \, \hat S_{\alpha \beta} \, g(\vec \xi_\beta, \vec y)$

Depending on the condition $\#t < \#s \text{ or } \#t \geq \#s$ we can now construct the rank-k-approximation as

$G_{|t \times s} \approx \left( A_b \, \hat S \right) \, B_b^* \quad \text{or}$

$G_{|t \times s} \approx A_b \, \left( B_b \,\hat S \right)^*$

with matrices

$\left( A_b \right)_{i\alpha} := \int_\Gamma \, \varphi(\vec x) \, g(\vec x, \vec \xi_\alpha) \, \mathrm d \vec x \quad ,$

$\left( B_b \right)_{j\beta} := \int_\Gamma \, g(\vec \xi_\beta, \vec y) \, \psi(\vec y) \, \mathrm d \vec y \quad .$

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of Chebyshev interpolation points in each spatial dimension.
accur	Assesses the minimum accuracy for the ACA approximation.

void setup_hmatrix_aprx_inter_col_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m
	)

This function initializes the bem2d object for approximating a matrix with tensorinterpolation within the column cluster.

The approximation of an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ is done by:

$G_{|t \times s} \approx A_{t,s} \, B_s^* \quad \text{with}$

$\left( A_{t,s} \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, g(\vec x , \, \vec \xi_\mu) \, \mathrm d \vec x \quad \text{and}$

$\left( B_s \right)_{j\mu} := \int_\Gamma \, \Lambda_\mu(\vec y) \, \psi_j(\vec y) \, \mathrm d \vec y \, .$

with $\Lambda$ being either the Lagrange polynomial $\mathcal L$ itself in case of single layer potential, or $\Lambda = \frac{\partial \mathcal L}{\partial n}$ in case of double layer potential.

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of Chebyshev interpolation points in each spatial dimension.

void setup_hmatrix_aprx_inter_mixed_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m
	)

This function initializes the bem2d object for approximating a matrix with tensorinterpolation within one of row or column cluster.

The interpolation depends on the condition:

$G_{|t \times s} \approx \begin{cases}\begin{array}{ll} A_t \, B_{t,s}^* &: \operatorname{diam}(t) <\operatorname{diam}(s)\\ A_{t,s} \, B_s^* &: \operatorname{diam}(t) \geq \operatorname{diam}(s) \end{array} \end{cases}$

For definition of these matrices see setup_hmatrix_aprx_inter_row_bem2d and setup_hmatrix_aprx_inter_col_bem2d .

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of Chebyshev interpolation points in each spatial dimension.

void setup_hmatrix_aprx_inter_row_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		uint	m
	)

This function initializes the bem2d object for approximating a matrix with tensorinterpolation within the row cluster.

The approximation of an admissible block $b = (t,s) \in \mathcal L_{\mathcal I \times \mathcal J}^+$ is done by:

$G_{|t \times s} \approx A_t \, B_{t,s}^* \quad \text{with}$

$\left( A_t \right)_{i\mu} := \int_\Gamma \, \varphi_i(\vec x) \, \mathcal L_\mu(\vec x) \, \mathrm d \vec x \quad \text{and}$

$\left( B_{t,s} \right)_{j\mu} := \int_\Gamma \, \gamma(\vec \xi_\mu , \, \vec y ) \, \psi_j(\vec y) \, \mathrm d \vec y \, .$

with $\gamma$ being the kernel function of the underlying integral operator. In case of the single layer potential this equal to the fundamental solution $ g $ , in case of double layer potential this applies to $\gamma = \frac{\partial g}{\partial n_y}$ .

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
m	Number of Chebyshev interpolation points in each spatial dimension.

void setup_hmatrix_aprx_paca_bem2d	(	pbem2d	bem,
		pccluster	rc,
		pccluster	cc,
		pcblock	tree,
		real	accur
	)

Approximate matrix block with ACA using partial pivoting.

This approximation scheme will utilize adaptive cross approximation with partial pivoting to retrieve a rank-k-approximation as

$G_{|t \times s} \approx A_b \, B_b^*$

with a given accuracy accur.

Parameters

bem	All needed callback functions and parameters for this approximation scheme are set within the bem object.
rc	Root of the row clustertree.
cc	Root of the column clustertree.
tree	Root of the blocktree.
accur	Assesses the minimum accuracy for the ACA approximation.

void setup_hmatrix_recomp_bem2d	(	pbem2d	bem,
		bool	recomp,
		real	accur_recomp,
		bool	coarsen,
		real	accur_coarsen
	)

Initialize the bem object for on the fly recompression techniques.

Parameters

bem	According to the other parameters within `bem->aprx` there are set some flags that indicate which of the recompression techniques should be used while building up a hmatrix .
recomp	If this flag is set to `true` a blockwise recompression will be applied. For each block $b = (t,s) \in \mathcal L^+$ independent on the approximation technique we will yield an approximation of the following kind: $G_{\|t \times s} \approx A B^* \quad A \in \mathbb K^{\hat t \times k} \, B \in \mathbb K^{\hat s \times k}$ After compression we yield a new rank-k-approximation holding $G_{\|t \times s} \approx \widetilde A \widetilde B^* \quad \widetilde A \in \mathbb K^{\hat t \times \widetilde k} \, \widetilde B \in \mathbb K^{\hat s \times \widetilde k}$ and $\widetilde k \leq k$ depending on the accuracy accur_recomp
accur_recomp	The accuracy the blockwise recompression will used to compress a block with SVD.
coarsen	If a block consists of $\tau$ sons which are all leafs of the blocktree, then it can be more efficient to store them as a single admissible leaf. This is done by "coarsening" recursively using the SVD.
accur_coarsen	The accuracy the coarsen technique will use to determine the coarsened block structure.

Data Structures

Typedefs

Enumerations

Functions

Detailed Description

Typedef Documentation

Enumeration Type Documentation

Function Documentation