 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
Lowest order Raviart-Thomas space on a two-dimensional triangular mesh. More...
Data Structures | |
| struct | _tri2drt0 |
| Representation of a trial space with lowest order Raviart-Thomas basis functions on a two-dimensional triangular mesh. More... | |
Typedefs | |
| typedef struct _tri2drt0 | tri2drt0 |
| Representation of a trial space with Raviart-Thomas edge basis functions on a two-dimensional triangular mesh. | |
| typedef tri2drt0 * | ptri2drt0 |
| Pointer to tri2drt0 object. | |
| typedef const tri2drt0 * | pctri2drt0 |
| Pointer to a constant tri2drt0 object. | |
Functions | |
| ptri2drt0 | new_tri2drt0 (pctri2d rt) |
| Create a tri2drt0 object using a tri2d mesh. More... | |
| void | update_tri2drt0 (ptri2drt0 rt0) |
| Update the numbers of degrees of freedoms and fixed edges after mixed boundary conditions were set. More... | |
| void | del_tri2drt0 (ptri2drt0 dc) |
| Delete a tri2drt0 object. More... | |
| psparsematrix | build_tri2drt0_A_sparsematrix (pctri2drt0 dc) |
| Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions and representing the upper left block of the saddle-point problem. More... | |
| psparsematrix | build_tri2drt0_B_sparsematrix (pctri2drt0 dc) |
| Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions for the flux and piecewise- constant functions for the pressure representing the lower left block of the saddle-point problem. More... | |
| psparsematrix | build_tri2drt0_A_interaction_sparsematrix (pctri2drt0 dc) |
| Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions and representing the upper left block of the saddle-point problem representing the interaction matrix. More... | |
| psparsematrix | build_tri2drt0_B_interaction_sparsematrix (pctri2drt0 dc) |
| Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions for the flux and piecewise- constant functions for the pressure representing the lower left block of the saddle-point problem representing the interaction matrix. More... | |
| void | assemble_tri2drt0_darcy_A_sparsematrix (pctri2drt0 dc, psparsematrix A, psparsematrix Af, pavector K) |
| Assemble the upper left block of the system matrix. More... | |
| void | assemble_tri2drt0_darcy_B_sparsematrix (pctri2drt0 dc, psparsematrix A, psparsematrix Af) |
| Assemble the lower left block of the system matrix. More... | |
| void | assemble_tri2drt0_b_D_avector (pctri2drt0 dc, field(*f)(const real *e, void *fdata), void *fdata, pavector d) |
| Discretize Dirichlet boundary values. More... | |
| void | assemble_tri2drt0_b_f_avector (ptri2drt0 dc, field(*f)(const real *x, void *fdata), void *fdata, pavector fv) |
Discretize an  -functional. More... -functional. More... | |
| void | assemble_tri2drt0_g_N_avector (ptri2drt0 dc, field(*f)(const uint *e, void *data), void *data, pavector g) |
| Discretize Neumann Boundary values. More... | |
| real | norml2_pressure_centroid_tri2drt0 (pctri2drt0 dc, field(*f)(const real *x, void *fdata), void *fdata, pcavector x2) |
Compute the  -norm of the discretization error for the pressure using the midpoint rule. More... -norm of the discretization error for the pressure using the midpoint rule. More... | |
| real | norml2_pressure_edgemidpoint_tri2drt0 (pctri2drt0 dc, field(*f)(const real *x, void *fdata), void *fdata, pcavector x2) |
Compute the  -norm of the discretization error for the pressure using the edge midpoint rule. More... -norm of the discretization error for the pressure using the edge midpoint rule. More... | |
| real | norml2_flux_centroid_tri2drt0 (pctri2drt0 dc, void(*f)(const real *x, void *fdata, pavector v), void *fdata, pcavector x1, pcavector g) |
Compute the  -norm of the discretization error for the flux using the midpoint rule. More... -norm of the discretization error for the flux using the midpoint rule. More... | |
| real | norml2_flux_edgemidpoint_tri2drt0 (pctri2drt0 dc, void(*f)(const real *x, void *fdata, pavector v), void *fdata, pcavector x1, pcavector g) |
Compute the  -norm of the discretization error for the flux using the edge midpoint rule. More... -norm of the discretization error for the flux using the edge midpoint rule. More... | |
| pclustergeometry | build_tri2drt0_A_clustergeometry (pctri2drt0 rt, uint *idx) |
| Create a clustergeometry object for the clustering ofthe degrees of freedom (edges). More... | |
| pclustergeometry | build_tri2drt0_B_clustergeometry (pctri2drt0 rt, uint *idx) |
| Create a clustergeometry object for the clustering of the triangles. More... | |
Lowest order Raviart-Thomas space on a two-dimensional triangular mesh.
E.g., this space is useful to discretize darcy's flow(Raviart-Thomas) and conservation of mass (piecewise constant functions), this leads to a saddle-point problem:
![\[ \begin{pmatrix} A & B^T\\ B & \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix} = \begin{pmatrix} b_D\\ b_f \end{pmatrix} \]](../../form_927.png)
| void assemble_tri2drt0_b_D_avector | ( | pctri2drt0 | dc, |
| field(*)(const real *e, void *fdata) | f, | ||
| void * | fdata, | ||
| pavector | d | ||
| ) |
Discretize Dirichlet boundary values.
For each Dirichlet edge, the function  is evaluated with the edge midpoint rule and the result is written to the corresponding entry in the result vector . For each non boundary edge the corresponding entry is zero.
is evaluated with the edge midpoint rule and the result is written to the corresponding entry in the result vector . For each non boundary edge the corresponding entry is zero.
| dc | tri2drt0 object describing the trial space. |
| f | Dirichlet boundary values. |
| fdata | Additional data for f. |
| d | Target vector of dimension dc->nfix. |
| void assemble_tri2drt0_b_f_avector | ( | ptri2drt0 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pavector | fv | ||
| ) |
Discretize an  -functional.
-functional.
For each triangle the entry of  is computed by applying the edge-midpoint quadrature. Since
is computed by applying the edge-midpoint quadrature. Since  is cleared before this step, the result is given by
is cleared before this step, the result is given by  .
.
| dc | tri2drt0 object describing the trial space. |
| f | Right-hand side function of the conservation of mass. |
| fdata | Additional data for f. |
| fv | Target vector of dimension dc->t2->triangles. |
| void assemble_tri2drt0_darcy_A_sparsematrix | ( | pctri2drt0 | dc, |
| psparsematrix | A, | ||
| psparsematrix | Af, | ||
| pavector | K | ||
| ) |
Assemble the upper left block of the system matrix.
Element matrices for all triangles are computed and added to the corresponding entries in A and Af.
| dc | tri2drt0 object describing the trial space. |
| A | Target matrix for degrees of freedom. |
| Af | Target matrix for interactions between fixed vertices and degrees of freedom. |
| K | Vector of length dc->t2->triangles filled with a (constant) permeability for each element |
| void assemble_tri2drt0_darcy_B_sparsematrix | ( | pctri2drt0 | dc, |
| psparsematrix | A, | ||
| psparsematrix | Af | ||
| ) |
Assemble the lower left block of the system matrix.
Element matrices for all triangles are computed and added to the corresponding entries in A and Af.
| dc | tri2drt0 object describing the trial space. |
| A | Target matrix for degrees of freedom. |
| Af | Target matrix for interactions between fixed vertices and degrees of freedom. |
| void assemble_tri2drt0_g_N_avector | ( | ptri2drt0 | dc, |
| field(*)(const uint *e, void *data) | f, | ||
| void * | data, | ||
| pavector | g | ||
| ) |
Discretize Neumann Boundary values.
Subtracting  resp.
resp.  from the right-hand side of our equation, where
from the right-hand side of our equation, where  resp.
resp.  is the interaction matrix, yields the right-hand side of the problem with Neumann boundary conditions.
is the interaction matrix, yields the right-hand side of the problem with Neumann boundary conditions.
| dc | tri2drt0 object describing the trial space. |
| f | Neumann Boundary values. |
| data | Additional data for f. |
| g | Target vector of dimension dc->nfix. |
| pclustergeometry build_tri2drt0_A_clustergeometry | ( | pctri2drt0 | rt, |
| uint * | idx | ||
| ) |
Create a clustergeometry object for the clustering ofthe degrees of freedom (edges).
Create a clustergeometry object basing on a triangular tri2d mesh and Raviart-Thomas functions.
| rt | tri2drt0 object. |
| idx | Array of indices (here: for the degrees of freedoms (edges)). |
| psparsematrix build_tri2drt0_A_interaction_sparsematrix | ( | pctri2drt0 | dc | ) |
Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions and representing the upper left block of the saddle-point problem representing the interaction matrix.
Creates a sparse matrix matching the Raviart-Thomas functions: if the supports of basis functions  and
and  share one triangle, the entry
share one triangle, the entry 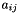 appears in the graph of the matrix.
appears in the graph of the matrix.
Here, only 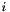 refers to a degree of freedom, while
refers to a degree of freedom, while  is the index of a fixed edge, i.e. has to be between
is the index of a fixed edge, i.e. has to be between 0 and nfix-1.
| dc | tri2drt0 object describing the space. |
dc->ndof rows and dc->nfix columns. | psparsematrix build_tri2drt0_A_sparsematrix | ( | pctri2drt0 | dc | ) |
Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions and representing the upper left block of the saddle-point problem.
Creates a sparse matrix matching the Raviart-Thomas functions: if the supports of basis functions  and
and  share at least one triangle, the entry
share at least one triangle, the entry 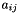 appears in the graph of the matrix.
appears in the graph of the matrix.
Here, both 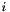 and
and  refer to degrees of freedom, i.e., there indices are between
refer to degrees of freedom, i.e., there indices are between 0 and ndof-1.
| dc | tri2drt0 object describing the space. |
dc->ndof rows and columns. | pclustergeometry build_tri2drt0_B_clustergeometry | ( | pctri2drt0 | rt, |
| uint * | idx | ||
| ) |
Create a clustergeometry object for the clustering of the triangles.
Create a clustergeometry object basing on a triangular tri2d mesh and linear nodal basis functions.
| rt | tri2drt0 object. |
| idx | Array of indices (here: for the triangles). |
| psparsematrix build_tri2drt0_B_interaction_sparsematrix | ( | pctri2drt0 | dc | ) |
Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions for the flux and piecewise- constant functions for the pressure representing the lower left block of the saddle-point problem representing the interaction matrix.
Creates a sparse matrix matching the Raviart-Thomas functions for the flux and piecewise-constant functions for the pressure: if the supports of basis functions  (pressure) and
(pressure) and  (flux) share at least one triangle, the entry
(flux) share at least one triangle, the entry 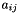 appears in the graph of the matrix.
appears in the graph of the matrix.
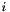 refers to the number of triangles in the mesh, i.e., the indices are between
refers to the number of triangles in the mesh, i.e., the indices are between 0 and dc->t2->triangles-1 and  is the index of a fixed edge, i.e. has to be between
is the index of a fixed edge, i.e. has to be between 0 and nfix-1.
| dc | tri2drt0 object describing the space. |
dc->t2->triangles rows anddc->nfix columns. | psparsematrix build_tri2drt0_B_sparsematrix | ( | pctri2drt0 | dc | ) |
Create a sparsematrix with a sparsity pattern matching the lowest order Raviart-Thomas functions for the flux and piecewise- constant functions for the pressure representing the lower left block of the saddle-point problem.
Creates a sparse matrix matching the Raviart-Thomas functions for the flux and piecewise-constant functions for the pressure: if the supports of basis functions  (pressure) and
(pressure) and  (flux) share at least one triangle, the entry
(flux) share at least one triangle, the entry 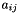 appears in the graph of the matrix.
appears in the graph of the matrix.
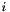 refers to the number of triangles in the mesh, i.e., the indices are between
refers to the number of triangles in the mesh, i.e., the indices are between 0 and dc->t2->triangles-1 and  refers to degrees of freedom,i.e., the indices are between
refers to degrees of freedom,i.e., the indices are between 0 and ndof-1.
| dc | tri2drt0 object describing the space. |
dc->t2->triangles rows anddc->ndof columns. | real norml2_flux_centroid_tri2drt0 | ( | pctri2drt0 | dc, |
| void(*)(const real *x, void *fdata, pavector v) | f, | ||
| void * | fdata, | ||
| pcavector | x1, | ||
| pcavector | g | ||
| ) |
Compute the  -norm of the discretization error for the flux using the midpoint rule.
-norm of the discretization error for the flux using the midpoint rule.
Compare the function f for the flux to the discrete function for the flux described by the vector x1 (for the degrees of freedom) and g (for the fixed Neumann edges). Measure the difference in the  -norm using the midpoint rule for approximation of the integral.
-norm using the midpoint rule for approximation of the integral.
| dc | tri2drt0 object describing the trial space. |
| f | Function. |
| fdata | Additional data for f. |
| x1 | Coefficients of the discrete function. |
| g | Coefficients of fixed parts of the discrete function. |
 -norm of the discretization error of the flux.
-norm of the discretization error of the flux. | real norml2_flux_edgemidpoint_tri2drt0 | ( | pctri2drt0 | dc, |
| void(*)(const real *x, void *fdata, pavector v) | f, | ||
| void * | fdata, | ||
| pcavector | x1, | ||
| pcavector | g | ||
| ) |
Compute the  -norm of the discretization error for the flux using the edge midpoint rule.
-norm of the discretization error for the flux using the edge midpoint rule.
Compare the function f for the flux to the discrete function for the flux described by the vector x1 (for the degrees of freedom) and g (for the fixed Neumann edges). Measure the difference in the  -norm using the edge midpoint rule for approximation of the integral.
-norm using the edge midpoint rule for approximation of the integral.
| dc | tri2drt0 object describing the trial space. |
| f | Function. |
| fdata | Additional data for f. |
| x1 | Coefficients of the discrete function. |
| g | Coefficients of fixed parts of the discrete function. |
 -norm of the discretization error of the flux.
-norm of the discretization error of the flux. | real norml2_pressure_centroid_tri2drt0 | ( | pctri2drt0 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pcavector | x2 | ||
| ) |
Compute the  -norm of the discretization error for the pressure using the midpoint rule.
-norm of the discretization error for the pressure using the midpoint rule.
Compare the pressure function f to the discrete function for the pressure described by the vector x2. Measure the difference in the  -norm using the midpoint rule for approximation of the integral.
-norm using the midpoint rule for approximation of the integral.
| dc | tri2drt0 object describing the trial space. |
| f | Function. |
| fdata | Additional data for f. |
| x2 | Coefficients of the discrete function. |
 -norm of the discretization error of the pressure.
-norm of the discretization error of the pressure. | real norml2_pressure_edgemidpoint_tri2drt0 | ( | pctri2drt0 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pcavector | x2 | ||
| ) |
Compute the  -norm of the discretization error for the pressure using the edge midpoint rule.
-norm of the discretization error for the pressure using the edge midpoint rule.
Compare the pressure function f to the discrete function for the pressure described by the vector x2. Measure the difference in the  -norm using the edge midpoint rule for approximation of the integral.
-norm using the edge midpoint rule for approximation of the integral.
| dc | tri2drt0 object describing the trial space. |
| f | Function. |
| fdata | Additional data for f. |
| x2 | Coefficients of the discrete function. |
 -norm of discretization error of the pressure.
-norm of discretization error of the pressure. | void update_tri2drt0 | ( | ptri2drt0 | rt0 | ) |
Update the numbers of degrees of freedoms and fixed edges after mixed boundary conditions were set.
Set the mixed boundary conditions in another function. Then the call of this functions updates the numbers and the numbering of degrees of freedoms and fixed edges.
| rt0 | This structure is updated. |
 1.8.11
1.8.11