 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
Representation of an 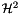 -matrix.
More...
-matrix.
More...
Data Structures | |
| struct | _h2matrix |
Representation of 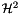 -matrices. More... -matrices. More... | |
| struct | _h2matrixlist |
| List of h2matrix objects. More... | |
Typedefs | |
| typedef struct _h2matrix | h2matrix |
Representation of an 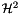 -matrix. -matrix. | |
| typedef h2matrix * | ph2matrix |
| Pointer to h2matrix object. | |
| typedef const h2matrix * | pch2matrix |
| Pointer to constant h2matrix object. | |
| typedef struct _h2matrixlist | h2matrixlist |
| List of h2matrix objects. | |
| typedef h2matrixlist * | ph2matrixlist |
| Pointer to h2matrixlist object. | |
| typedef const h2matrixlist * | pch2matrixlist |
| Pointer to constant h2matrixlist object. | |
| typedef void(* | h2matrix_callback_t) (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, void *data) |
| Callback function for h2matrix iterators. More... | |
| typedef void(* | h2matrixlist_callback_t) (pccluster t, uint tname, uint pardepth, pch2matrixlist hl, void *data) |
| Callback function for h2matrixlist iterators. More... | |
Functions | |
| ph2matrix | new_h2matrix (pclusterbasis rb, pclusterbasis cb) |
| Create a new h2matrix object. More... | |
| ph2matrix | new_uniform_h2matrix (pclusterbasis rb, pclusterbasis cb) |
| Create a new h2matrix object representing a uniform matrix. More... | |
| ph2matrix | new_full_h2matrix (pclusterbasis rb, pclusterbasis cb) |
| Create a new h2matrix object representing a standard dense matrix. More... | |
| ph2matrix | new_super_h2matrix (pclusterbasis rb, pclusterbasis cb, uint rsons, uint csons) |
| Create a new hmatrix object representing a subdivided matrix. More... | |
| ph2matrix | new_zero_h2matrix (pclusterbasis rb, pclusterbasis cb) |
| Create a new h2matrix object representing a zero matrix. More... | |
| ph2matrix | clonestructure_h2matrix (pch2matrix h2, pclusterbasis rb, pclusterbasis cb) |
Builds a new h2matrix with clusterbasis rb and cb and the block structure of h2. More... | |
| ph2matrix | clone_h2matrix (pch2matrix h2, pclusterbasis rb, pclusterbasis cb) |
Builds a new h2matrix with clusterbasis rb and cb and the block structure of h2. Copies all coupling matrices  to the clone. More... to the clone. More... | |
| void | update_h2matrix (ph2matrix h2) |
| Complete the initialisation of a h2matrix object. More... | |
| void | del_h2matrix (ph2matrix h2) |
| Delete an h2matrix object. More... | |
| void | ref_h2matrix (ph2matrix *ptr, ph2matrix h2) |
| Set a pointer to an h2matrix object, increase its reference counter, and decrease reference counter of original pointer target. More... | |
| void | unref_h2matrix (ph2matrix h2) |
| Reduce the reference counter of an h2matrix object. More... | |
| size_t | getsize_h2matrix (pch2matrix h2) |
| Get size of a given h2matrix object. More... | |
| size_t | gettotalsize_h2matrix (pch2matrix h2) |
| Get total size of a given h2matrix object, including cluster bases. More... | |
| size_t | getnearsize_h2matrix (pch2matrix h2) |
| Get size of the nearfield part of a given h2matrix object. More... | |
| size_t | getfarsize_h2matrix (pch2matrix h2) |
| Get size of the farfield part of a given h2matrix object. More... | |
| void | clear_h2matrix (ph2matrix h2) |
| Set an h2matrix to zero by clearing all far- and nearfield matrices. More... | |
| void | scale_h2matrix (field alpha, ph2matrix h2) |
| Scale an h2matrix by a factor. More... | |
| void | random_h2matrix (ph2matrix h2) |
| Fill an h2matrix with random coefficients. More... | |
| ph2matrix | build_from_block_h2matrix (pcblock b, pclusterbasis rb, pclusterbasis cb) |
| Build an h2matrix object from a block tree using given cluster bases. More... | |
| pblock | build_from_h2matrix_block (pch2matrix G) |
| Build an block tree from an h2matrix. More... | |
| ph2matrix * | enumerate_h2matrix (ph2matrix h2) |
| Enumerate h2matrix according to block tree. More... | |
| void | iterate_h2matrix (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, h2matrix_callback_t pre, h2matrix_callback_t post, void *data) |
| Iterate through all submatrices of an h2matrix. More... | |
| void | iterate_rowlist_h2matrix (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, h2matrixlist_callback_t pre, h2matrixlist_callback_t post, void *data) |
| Iterate through all submatrices of an h2matrix, collecting all row blocks in an h2matrixlist object. More... | |
| void | iterate_collist_h2matrix (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, h2matrixlist_callback_t pre, h2matrixlist_callback_t post, void *data) |
| Iterate through all submatrices of an h2matrix, collecting all column blocks in an h2matrixlist object. More... | |
| void | iterate_byrow_h2matrix (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, h2matrix_callback_t pre, h2matrix_callback_t post, void *data) |
| Iterate through all submatrices of an h2matrix. More... | |
| void | iterate_bycol_h2matrix (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, h2matrix_callback_t pre, h2matrix_callback_t post, void *data) |
| Iterate through all submatrices of an h2matrix. More... | |
| void | mvm_h2matrix_avector (field alpha, bool h2trans, pch2matrix h2, pcavector x, pavector y) |
Matrix-vector multiplication  or or  . More... . More... | |
| void | fastaddeval_h2matrix_avector (field alpha, pch2matrix h2, pavector xt, pavector yt) |
| Interaction phase of the matrix-vector multiplication. More... | |
| void | addeval_h2matrix_avector (field alpha, pch2matrix h2, pcavector x, pavector y) |
Matrix-vector multiplication  . More... . More... | |
| void | fastaddevaltrans_h2matrix_avector (field alpha, pch2matrix h2, pavector xt, pavector yt) |
| Interaction phase of the adjoint matrix-vector multiplication. More... | |
| void | addevaltrans_h2matrix_avector (field alpha, pch2matrix h2, pcavector x, pavector y) |
Adjoint matrix-vector multiplication  . More... . More... | |
| void | addevalsymm_h2matrix_avector (field alpha, pch2matrix h2, pcavector x, pavector y) |
Symmetric matrix-vector multiplication,  , where , where  is assumed to be self-adjoint and only its lower triangular part is used. More... is assumed to be self-adjoint and only its lower triangular part is used. More... | |
| void | fastaddmul_h2matrix_amatrix_amatrix (field alpha, bool atrans, pch2matrix A, pcamatrix Bt, pamatrix Ct) |
| Interaction phase of the h2matrix - amatrix multiplication. More... | |
| void | addmul_h2matrix_amatrix_amatrix (field alpha, bool atrans, pch2matrix A, bool btrans, pcamatrix B, pamatrix C) |
Matrix multiplication  , ,  , ,  or or  . More... . More... | |
| void | addmul_amatrix_h2matrix_amatrix (field alpha, bool atrans, pcamatrix A, bool btrans, pch2matrix B, pamatrix C) |
Matrix multiplication  , ,  , ,  or or  . More... . More... | |
| void | collectdense_h2matrix (pcamatrix a, pcclusterbasis rb, pcclusterbasis cb, pamatrix s) |
Compute  . More... . More... | |
| void | project_amatrix_h2matrix (ph2matrix h2, pcamatrix a) |
Compute the best approximation of a given matrix  with respect to an with respect to an 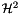 -matrix space. More... -matrix space. More... | |
| void | project_hmatrix_h2matrix (ph2matrix h2, phmatrix h) |
Compute the best approximation of a given matrix  with respect to an with respect to an 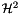 -matrix space. More... -matrix space. More... | |
| real | norm2_h2matrix (pch2matrix H2) |
Approximate the spectral norm  of a matrix of a matrix  . More... . More... | |
| real | norm2diff_h2matrix (pch2matrix a, pch2matrix b) |
Approximate the spectral norm  of the difference of two matrices of the difference of two matrices  and and 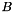 . More... . More... | |
| void | write_cdf_h2matrix (pch2matrix G, const char *name) |
| Write h2matrix to NetCDF file. More... | |
| void | write_cdfpart_h2matrix (pch2matrix G, int nc_file, const char *prefix) |
| Write h2matrix to part of a NetCDF file. More... | |
| ph2matrix | read_cdf_h2matrix (const char *name, pclusterbasis rb, pclusterbasis cb) |
| Read h2matrix from NetCDF file. More... | |
| ph2matrix | read_cdfpart_h2matrix (int nc_file, const char *prefix, pclusterbasis rb, pclusterbasis cb) |
| Read h2matrix from part of a NetCDF file. More... | |
| void | write_cdfcomplete_h2matrix (pch2matrix G, const char *name) |
| Write h2matrix to NetCDF file, including cluster trees and cluster bases. More... | |
| ph2matrix | read_cdfcomplete_h2matrix (const char *name) |
| Read h2matrix from NetCDF file, including cluster trees and cluster bases. More... | |
| void | draw_cairo_h2matrix (cairo_t *cr, pch2matrix G, bool storage, uint levels) |
| Draw a h2matrix to a cairo surface. More... | |
| uint | getrows_h2matrix (pch2matrix h2) |
Get the number of rows of an h2matrix  . More... . More... | |
| uint | getcols_h2matrix (pch2matrix h2) |
Get the number of columns of an h2matrix  . More... . More... | |
Representation of an 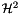 -matrix.
-matrix.
The h2matrix class is used to represent 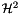 -matrices with arbitrary block structures and arbitrary cluster bases.
-matrices with arbitrary block structures and arbitrary cluster bases.
| typedef void(* h2matrix_callback_t) (ph2matrix G, uint mname, uint rname, uint cname, uint pardepth, void *data) |
Callback function for h2matrix iterators.
| G | Matrix. |
| mname | Number of matrix. |
| rname | Number of row cluster. |
| cname | Number of column cluster. |
| pardepth | Parallelization depth. |
| data | Additional data. |
| typedef void(* h2matrixlist_callback_t) (pccluster t, uint tname, uint pardepth, pch2matrixlist hl, void *data) |
Callback function for h2matrixlist iterators.
| t | Cluster. |
| tname | Number of cluster. |
| pardepth | Parallelization depth. |
| hl | List of h2matrix objects. |
| data | Additional data. |
| void addeval_h2matrix_avector | ( | field | alpha, |
| pch2matrix | h2, | ||
| pcavector | x, | ||
| pavector | y | ||
| ) |
Matrix-vector multiplication  .
.
The matrix is multiplied by the source vector 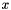 , the result is scaled by
, the result is scaled by 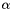 and added to the target vector
and added to the target vector 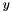 .
.
| alpha | Scaling factor 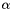 . . |
| h2 | Matrix  . . |
| x | Source vector 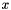 . . |
| y | Target vector 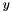 . . |
| void addevalsymm_h2matrix_avector | ( | field | alpha, |
| pch2matrix | h2, | ||
| pcavector | x, | ||
| pavector | y | ||
| ) |
Symmetric matrix-vector multiplication,  , where
, where  is assumed to be self-adjoint and only its lower triangular part is used.
is assumed to be self-adjoint and only its lower triangular part is used.
| alpha | Scaling factor 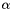 . . |
| h2 | Matrix  . . |
| x | Source vector 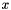 . . |
| y | Target vector 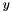 . . |
| void addevaltrans_h2matrix_avector | ( | field | alpha, |
| pch2matrix | h2, | ||
| pcavector | x, | ||
| pavector | y | ||
| ) |
Adjoint matrix-vector multiplication  .
.
The adjoint matrix is multiplied by the source vector 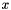 , the result is scaled by
, the result is scaled by 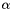 and added to the target vector
and added to the target vector 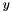 .
.
| alpha | Scaling factor 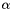 . . |
| h2 | Matrix  . . |
| x | Source vector 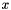 . . |
| y | Target vector 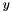 . . |
| void addmul_amatrix_h2matrix_amatrix | ( | field | alpha, |
| bool | atrans, | ||
| pcamatrix | A, | ||
| bool | btrans, | ||
| pch2matrix | B, | ||
| pamatrix | C | ||
| ) |
Matrix multiplication  ,
,  ,
,  or
or  .
.
Multiplies an amatrix by an h2matrix. For the truncated multiplication of two h2matrix objects, see addmul_h2matrix.
| void addmul_h2matrix_amatrix_amatrix | ( | field | alpha, |
| bool | atrans, | ||
| pch2matrix | A, | ||
| bool | btrans, | ||
| pcamatrix | B, | ||
| pamatrix | C | ||
| ) |
Matrix multiplication  ,
,  ,
,  or
or  .
.
Multiplies an h2matrix by an amatrix. For the truncated multiplication of two h2matrix objects, see addmul_h2matrix.
| ph2matrix build_from_block_h2matrix | ( | pcblock | b, |
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
| pblock build_from_h2matrix_block | ( | pch2matrix | G | ) |
| void clear_h2matrix | ( | ph2matrix | h2 | ) |
Set an h2matrix to zero by clearing all far- and nearfield matrices.
| h2 | Target matrix. |
| ph2matrix clone_h2matrix | ( | pch2matrix | h2, |
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
Builds a new h2matrix with clusterbasis rb and cb and the block structure of h2. Copies all coupling matrices  to the clone.
to the clone.
| h2 | Input h2matrix which has to be cloned. |
| rb | Row clusterbasis for the clone. |
| cb | Column clusterbasis for the clone. |
rb and cb and the same data as h2. | ph2matrix clonestructure_h2matrix | ( | pch2matrix | h2, |
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
Builds a new h2matrix with clusterbasis rb and cb and the block structure of h2.
| h2 | Input h2matrix whose structure has to be cloned. |
| rb | Row clusterbasis for the clone. |
| cb | Column clusterbasis for the clone. |
rb and cb and the same block structure as h2. | void collectdense_h2matrix | ( | pcamatrix | a, |
| pcclusterbasis | rb, | ||
| pcclusterbasis | cb, | ||
| pamatrix | s | ||
| ) |
Compute  .
.
If row and column basis are orthogonal, the result is the coupling matrix for the optimal approximation of  in these bases with respect to the spectral and Frobenius norms.
in these bases with respect to the spectral and Frobenius norms.
| a | Source matrix  . . |
| rb | Row basis  . . |
| cb | Column basis  . . |
| s | Target matrix, will be overwritten by  . . |
| void del_h2matrix | ( | ph2matrix | h2 | ) |
Delete an h2matrix object.
Releases the storage corresponding to the object. If this h2matrix contains pointers to submatrices, the submatrices are released by unref_h2matrix.
Only objects with h2->refs==0 may be deleted.
| h2 | Object to be deleted. |
| void draw_cairo_h2matrix | ( | cairo_t * | cr, |
| pch2matrix | G, | ||
| bool | storage, | ||
| uint | levels | ||
| ) |
Draw a h2matrix to a cairo surface.
Enumerate h2matrix according to block tree.
The h2matrix submatrices are enumerated in an array of size h2->desc. The enumeration starts with 0 assigned to the root and then proceeds column-wise starting with b->sons[0] corresponding to the entries 1 to h2->sons[0]->desc in the array and ending with h2->sons[rsons*csons-1] corresponding to the last b->sons[rsons*csons-1]->desc entries.
| h2 | Matrix matching the block structure given by b. |
h2->desc containing pointers to the h2matrix objects corresponding to descendants of h2. | void fastaddeval_h2matrix_avector | ( | field | alpha, |
| pch2matrix | h2, | ||
| pavector | xt, | ||
| pavector | yt | ||
| ) |
Interaction phase of the matrix-vector multiplication.
Nearfield blocks are added directly  , farfield block contributions are accumulated
, farfield block contributions are accumulated  .
.
Both xt and yt should be coefficient vectors provided by new_coeffs_clusterbasis_avector, xt is usually initialized by forward_clusterbasis_avector, while yt is typically added to the result using backward_clusterbasis_avector.
| alpha | Scaling factor 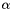 . . |
| h2 | Matrix  . . |
| xt | Coefficients  of the source vector with respect to the column basis of the source vector with respect to the column basis h2->cb. |
| yt | Coefficients  of the target vector with respect to the row basis of the target vector with respect to the row basis h2->rb. |
| void fastaddevaltrans_h2matrix_avector | ( | field | alpha, |
| pch2matrix | h2, | ||
| pavector | xt, | ||
| pavector | yt | ||
| ) |
Interaction phase of the adjoint matrix-vector multiplication.
Nearfield blocks are added directly  , farfield block contributions are accumulated
, farfield block contributions are accumulated  .
.
Both xt and yt should be coefficient vectors provided by new_coeffs_clusterbasis_avector, xt is usually initialized by forward_clusterbasis_avector, while yt is typically added to the result using backward_clusterbasis_avector.
| alpha | Scaling factor 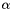 . . |
| h2 | Matrix  . . |
| xt | Coefficients  of the source vector with respect to the row basis of the source vector with respect to the row basis h2->rb. |
| yt | Coefficients  of the target vector with respect to the column basis of the target vector with respect to the column basis h2->cb. |
| void fastaddmul_h2matrix_amatrix_amatrix | ( | field | alpha, |
| bool | atrans, | ||
| pch2matrix | A, | ||
| pcamatrix | Bt, | ||
| pamatrix | Ct | ||
| ) |
Interaction phase of the h2matrix - amatrix multiplication.
If atrans==false, nearfield blocks are added directly  , farfield block contributions are accumulated
, farfield block contributions are accumulated  . Both
. Both bt and ct should be coefficient matrices with the same number of columns and cb->ktree and rb->ktree rows, respectively.
If atrans==true, nearfield blocks are treated by  , farfield block contributions are accumulated
, farfield block contributions are accumulated  . Both
. Both bt and ct should be coefficient matrices with the same number of columns and rb->ktree and cb->ktree rows, respectively.
bt is usually initialized by forward_clusterbasis_amatrix, while ct is typically added to the result using backward_clusterbasis_amatrix.
| alpha | Scaling factor 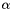 . . |
| atrans | Set if  is to be used instead of is to be used instead of  . . |
| A | First source matrix  . . |
| Bt | Second source matrix, expressed through coefficient matrices  of the second source matrix with respect to the column basis of the second source matrix with respect to the column basis h2->cb if atrans==false and through  with respect to the row basis with respect to the row basis h2->rb otherwise. |
| Ct | Target matrix, expressed through coefficient matrices  with respect to the row basis with respect to the row basis h2->rb if atrans==false and through  with respect to the column basis with respect to the column basis h2->cb otherwise. |
| uint getcols_h2matrix | ( | pch2matrix | h2 | ) |
| size_t getfarsize_h2matrix | ( | pch2matrix | h2 | ) |
Get size of the farfield part of a given h2matrix object.
| h2 | 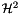 -matrix object. -matrix object. |
| size_t getnearsize_h2matrix | ( | pch2matrix | h2 | ) |
Get size of the nearfield part of a given h2matrix object.
| h2 | 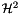 -matrix object. -matrix object. |
| uint getrows_h2matrix | ( | pch2matrix | h2 | ) |
| size_t getsize_h2matrix | ( | pch2matrix | h2 | ) |
Get size of a given h2matrix object.
| h2 | 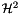 -matrix object. -matrix object. |
| size_t gettotalsize_h2matrix | ( | pch2matrix | h2 | ) |
Get total size of a given h2matrix object, including cluster bases.
| h2 | 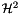 -matrix object. -matrix object. |
| void iterate_bycol_h2matrix | ( | ph2matrix | G, |
| uint | mname, | ||
| uint | rname, | ||
| uint | cname, | ||
| uint | pardepth, | ||
| h2matrix_callback_t | pre, | ||
| h2matrix_callback_t | post, | ||
| void * | data | ||
| ) |
Iterate through all submatrices of an h2matrix.
If the iterator works with multiple threads, it guarantees that threads running in parallel call the pre and post functions with different column clusters.
| G | Matrix. |
| mname | Number of matrix block. |
| rname | Number of row cluster. |
| cname | Number of column cluster. |
| pardepth | Parallization depth. |
| pre | Function called before accessing sons. |
| post | Function called after accessing sons. |
| data | Additional data passed to callback functions. |
| void iterate_byrow_h2matrix | ( | ph2matrix | G, |
| uint | mname, | ||
| uint | rname, | ||
| uint | cname, | ||
| uint | pardepth, | ||
| h2matrix_callback_t | pre, | ||
| h2matrix_callback_t | post, | ||
| void * | data | ||
| ) |
Iterate through all submatrices of an h2matrix.
If the iterator works with multiple threads, it guarantees that threads running in parallel call the pre and post functions with different row clusters.
| G | Matrix. |
| mname | Number of matrix block. |
| rname | Number of row cluster. |
| cname | Number of column cluster. |
| pardepth | Parallization depth. |
| pre | Function called before accessing sons. |
| post | Function called after accessing sons. |
| data | Additional data passed to callback functions. |
| void iterate_collist_h2matrix | ( | ph2matrix | G, |
| uint | mname, | ||
| uint | rname, | ||
| uint | cname, | ||
| uint | pardepth, | ||
| h2matrixlist_callback_t | pre, | ||
| h2matrixlist_callback_t | post, | ||
| void * | data | ||
| ) |
Iterate through all submatrices of an h2matrix, collecting all column blocks in an h2matrixlist object.
| G | Matrix. |
| mname | Number of matrix block. |
| rname | Number of row cluster. |
| cname | Number of column cluster. |
| pardepth | Parallization depth. |
| pre | Function called before accessing sons. |
| post | Function called after accessing sons. |
| data | Additional data passed to callback functions. |
| void iterate_h2matrix | ( | ph2matrix | G, |
| uint | mname, | ||
| uint | rname, | ||
| uint | cname, | ||
| uint | pardepth, | ||
| h2matrix_callback_t | pre, | ||
| h2matrix_callback_t | post, | ||
| void * | data | ||
| ) |
Iterate through all submatrices of an h2matrix.
If the iterator works with multiple threads, it guarantees that threads running in parallel call the pre and post functions with different row and column clusters.
| G | Matrix. |
| mname | Number of matrix block. |
| rname | Number of row cluster. |
| cname | Number of column cluster. |
| pardepth | Parallization depth. |
| pre | Function called before accessing sons. |
| post | Function called after accessing sons. |
| data | Additional data passed to callback functions. |
| void iterate_rowlist_h2matrix | ( | ph2matrix | G, |
| uint | mname, | ||
| uint | rname, | ||
| uint | cname, | ||
| uint | pardepth, | ||
| h2matrixlist_callback_t | pre, | ||
| h2matrixlist_callback_t | post, | ||
| void * | data | ||
| ) |
Iterate through all submatrices of an h2matrix, collecting all row blocks in an h2matrixlist object.
| G | Matrix. |
| mname | Number of matrix block. |
| rname | Number of row cluster. |
| cname | Number of column cluster. |
| pardepth | Parallization depth. |
| pre | Function called before accessing sons. |
| post | Function called after accessing sons. |
| data | Additional data passed to callback functions. |
| void mvm_h2matrix_avector | ( | field | alpha, |
| bool | h2trans, | ||
| pch2matrix | h2, | ||
| pcavector | x, | ||
| pavector | y | ||
| ) |
Matrix-vector multiplication  or
or  .
.
The matrix or its adjoint is multiplied by the source vector 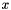 , the result is scaled by
, the result is scaled by 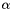 and added to the target vector
and added to the target vector 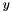 .
.
| alpha | Scaling factor 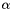 . . |
| h2trans | Set if  is to be used instead of is to be used instead of  . . |
| h2 | Matrix  . . |
| x | Source vector 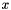 . . |
| y | Target vector 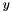 . . |
| ph2matrix new_full_h2matrix | ( | pclusterbasis | rb, |
| pclusterbasis | cb | ||
| ) |
Create a new h2matrix object representing a standard dense matrix.
Allocates storage for the object containing an amatrix object.
| rb | Row cluster basis. |
| cb | Column cluster basis. |
| ph2matrix new_h2matrix | ( | pclusterbasis | rb, |
| pclusterbasis | cb | ||
| ) |
Create a new h2matrix object.
Allocates storage for the object and sets the matrix pointers to NULL, representing a zero matrix.
| rb | Row cluster basis. |
| cb | Column cluster basis. |
| ph2matrix new_super_h2matrix | ( | pclusterbasis | rb, |
| pclusterbasis | cb, | ||
| uint | rsons, | ||
| uint | csons | ||
| ) |
Create a new hmatrix object representing a subdivided matrix.
Allocates storage for the object representing a matrix with submatrices. The submatrices are initialized with NULL pointers and have to be set up with ref_hmatrix.
| rb | Row cluster basis. |
| cb | Column cluster basis. |
| rsons | Number of block rows. |
| csons | Number of block columns. |
| ph2matrix new_uniform_h2matrix | ( | pclusterbasis | rb, |
| pclusterbasis | cb | ||
| ) |
Create a new h2matrix object representing a uniform matrix.
Allocates storage for the object containing a uniform object.
| rb | Row cluster basis. |
| cb | Column cluster basis. |
| ph2matrix new_zero_h2matrix | ( | pclusterbasis | rb, |
| pclusterbasis | cb | ||
| ) |
Create a new h2matrix object representing a zero matrix.
Allocates storage for the object representing a zero matrix.
| rb | Row cluster basis. |
| cb | Column cluster basis. |
| real norm2_h2matrix | ( | pch2matrix | H2 | ) |
Approximate the spectral norm  of a matrix
of a matrix  .
.
The spectral norm is approximated by applying a few steps of the power iteration to the matrix  and computing the square root of the resulting eigenvalue approximation.
and computing the square root of the resulting eigenvalue approximation.
| H2 |  matrix matrix  . . |
 .
. | real norm2diff_h2matrix | ( | pch2matrix | a, |
| pch2matrix | b | ||
| ) |
Approximate the spectral norm  of the difference of two matrices
of the difference of two matrices  and
and  .
.
The spectral norm is approximated by applying a few steps of the power iteration to the matrix  and computing the square root of the resulting eigenvalue approximation.
and computing the square root of the resulting eigenvalue approximation.
| a |  matrix matrix  . . |
| b |  matrix matrix  . . |
 .
. Compute the best approximation of a given matrix  with respect to an
with respect to an 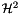 -matrix space.
-matrix space.
All nearfield blocks will be copied (and permuted according to the cluster numbering), all farfield blocks will be approximated by coupling matrices  .
.
h2->rb and the column basis h2->cb should be orthogonal.| h2 | Target matrix, will be overwritten by the best approximation of the source matrix. |
| a | Source matrix. |
Compute the best approximation of a given matrix  with respect to an
with respect to an 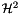 -matrix space.
-matrix space.
All nearfield blocks will be copied (and permuted according to the cluster numbering), all farfield blocks  will be approximated by coupling matrices
will be approximated by coupling matrices  .
.
h2->rb and the column basis h2->cb should be orthogonal.| h2 | Target matrix, will be overwritten by the best approximation of the source matrix. |
| h | Source matrix. |
| void random_h2matrix | ( | ph2matrix | h2 | ) |
Fill an h2matrix with random coefficients.
| h2 | Target matrix  . . |
| ph2matrix read_cdf_h2matrix | ( | const char * | name, |
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
| ph2matrix read_cdfcomplete_h2matrix | ( | const char * | name | ) |
| ph2matrix read_cdfpart_h2matrix | ( | int | nc_file, |
| const char * | prefix, | ||
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
Scale an h2matrix by a factor.
| alpha | Scaling factor 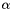 . . |
| h2 | Target matrix  , will be overwritten by , will be overwritten by  . . |
| void unref_h2matrix | ( | ph2matrix | h2 | ) |
Reduce the reference counter of an h2matrix object.
If the reference counter reaches zero, the object is deleted.
h2=NULL instead, since this guarantees that the pointer is properly invalidated.| h2 | h2matrix that will be unreferenced. |
| void update_h2matrix | ( | ph2matrix | h2 | ) |
| void write_cdf_h2matrix | ( | pch2matrix | G, |
| const char * | name | ||
| ) |
Write h2matrix to NetCDF file.
| G | Matrix. |
| name | File name. |
| void write_cdfcomplete_h2matrix | ( | pch2matrix | G, |
| const char * | name | ||
| ) |
Write h2matrix to NetCDF file, including cluster trees and cluster bases.
| G | Matrix. |
| name | File name. |
| void write_cdfpart_h2matrix | ( | pch2matrix | G, |
| int | nc_file, | ||
| const char * | prefix | ||
| ) |
Write h2matrix to part of a NetCDF file.
| G | Matrix. |
| nc_file | File handle. |
| prefix | Prefix for variable names. |
 1.8.11
1.8.11