 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
#include "settings.h"Go to the source code of this file.
Macros | |
| #define | h2_dot(n, x, incx, y, incy) zdotc_(n, x, incx, y, incy) |
Compute the dot product of two field vectors  and and  of length of length n. More... | |
| #define | h2_rdot(n, x, incx, y, incy) ddot_(n, x, incx, y, incy) |
Compute the dot product of two real vectors  and and  of length of length n. More... | |
| #define | h2_axpy(n, alpha, x, incx, y, incy) zaxpy_(n, alpha, x, incx, y, incy) |
Add a field vector  to another field vector to another field vector  . More... . More... | |
| #define | h2_raxpy(n, alpha, x, incx, y, incy) daxpy_(n, alpha, x, incx, y, incy) |
Add a real vector  to another field vector to another field vector  . More... . More... | |
| #define | h2_scal(n, alpha, x, incx) zscal_(n, alpha, x, incx) |
Scales a field vector  by a field scalar by a field scalar 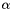 . More... . More... | |
| #define | h2_rscal(n, alpha, x, incx) zdscal_(n, alpha, x, incx) |
Scales a field vector  by a real scalar by a real scalar 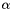 . More... . More... | |
| #define | h2_nrm2(n, x, incx) dznrm2_(n, x, incx) |
Computes the 2-norm  of a field vector of a field vector  . More... . More... | |
| #define | h2_swap(n, x, incx, y, incy) zswap_(n, x, incx, y, incy) |
Swaps to entries of two field vectors  and and  . More... . More... | |
| #define | h2_gemv(trans, m, n, alpha, a, lda, x, incx, beta, y, incy) zgemv_(trans, m, n, alpha, a, lda, x, incx, beta, y, incy) |
Compute matrix vector product of a general matrix  with input vector with input vector  and output vector and output vector 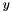 . More... . More... | |
| #define | h2_trmv(uplo, trans, diag, n, a, lda, x, incx) ztrmv_(uplo, trans, diag, n, a, lda, x, incx) |
Compute matrix vector product of a triangular matrix  with input and output vector with input and output vector  . More... . More... | |
| #define | h2_ger(m, n, alpha, x, incx, y, incy, a, lda) zgerc_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_gerc(m, n, alpha, x, incx, y, incy, a, lda) zgerc_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_geru(m, n, alpha, x, incx, y, incy, a, lda) zgeru_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_syr(uplo, n, alpha, x, incx, a, lda) zher_(uplo, n, alpha, x, incx, a, lda) |
Adds a symmetric/hermetian rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_gemm(transa, transb, m, n, k, alpha, a, lda, b, ldb, beta, c, ldc) zgemm_(transa, transb, m, n, k, alpha, a, lda, b, ldb, beta, c, ldc) |
Compute matrix-matrix-multiplication for general matrices  and and  . More... . More... | |
| #define | h2_trmm(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) ztrmm_(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
Compute matrix-matrix-multiplication for triangular matrices  and a general matrix and a general matrix 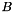 . More... . More... | |
| #define | h2_trsm(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) ztrsm_(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
Solves a linear system of equations with a triangular matrix  and a right-hand-side matrix and a right-hand-side matrix 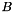 . More... . More... | |
| #define | h2_lacgv(n, x, incx) zlacgv_(n, x, incx) |
Conjugates a vector of field  . More... . More... | |
| #define | h2_potrf(uplo, n, a, lda, info) zpotrf_(uplo, n, a, lda, info) |
Computes the Cholesky factorization of symmetric/hermitian positive definite matrix  in-place. More... in-place. More... | |
| #define | h2_larf(side, m, n, v, incv, tau, c, ldc, work) zlarf_(side, m, n, v, incv, tau, c, ldc, work) |
Applies an elementary reflector  to a matrix to a matrix  . More... . More... | |
| #define | h2_larfg(n, alpha, x, incx, tau) zlarfg_(n, alpha, x, incx, tau) |
Create an elementary reflector  . More... . More... | |
| #define | h2_geqrf(m, n, a, lda, tau, work, lwork, info) zgeqrf_(m, n, a, lda, tau, work, lwork, info) |
Compute a QR-decomposition of the matrix  . More... . More... | |
| #define | h2_ormqr(side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info) zunmqr_(side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info) |
Apply orthogonal/unitary matrix  from "Left" or from "Right" to a matrix from "Left" or from "Right" to a matrix  . More... . More... | |
| #define | h2_orgqr(m, n, k, a, lda, tau, work, lwork, info) zungqr_(m, n, k, a, lda, tau, work, lwork, info) |
Generate the orthogonal/unitary matrix  out of its elementary reflectors out of its elementary reflectors  . More... . More... | |
| #define | h2_steqr(compz, n, d, e, z, ldz, work, info) zsteqr_(compz, n, d, e, z, ldz, work, info) |
Compute all eigenvalues and optionally all eigenvectors of a symmetric tridiagonal matrix  using implicit QL or QR method. More... using implicit QL or QR method. More... | |
| #define | h2_stev(jobz, n, d, e, z, ldz, work, info) dstev_(jobz, n, d, e, z, ldz, work, info) |
Compute all eigenvalues and optionally all eigenvectors of a real symmetric tridiagonal matrix  . More... . More... | |
| #define | h2_gesvd(jobu, jobvt, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, info) zgesvd_(jobu, jobvt, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, info) |
Compute the SVD of a general matrix  . More... . More... | |
| #define | h2_bdsqr(uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info) zbdsqr_(uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info) |
Compute the SVD of a real "Lower" or "Upper" bidiagonal matrix 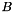 . More... . More... | |
| #define | h2_heev(jobz, uplo, n, a, lda, w, work, lwork, rwork, info) zheev_(jobz, uplo, n, a, lda, w, work, lwork, rwork, info) |
Compute all eigenvalues and optionally all eigenvectors of a hermitian / symmetric matrix  . More... . More... | |
 1.8.11
1.8.11