 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
Piecewise linear space with nodal basis functions on a three-dimensional tetrahedral mesh. More...
Data Structures | |
| struct | _tet3dp1 |
| Representation of a trial space with piecewise linear nodal basis functions on a three-dimensional tetrahedral mesh. More... | |
Typedefs | |
| typedef struct _tet3dp1 | tet3dp1 |
| Representation of a trial space with piecewise linear nodal basis functions on a three-dimensional tetrahedral mesh. | |
| typedef tet3dp1 * | ptet3dp1 |
| Pointer to a tet3dp1 object. | |
| typedef const tet3dp1 * | pctet3dp1 |
| Pointer to a constant tet3dp1 object. | |
Functions | |
| ptet3dp1 | new_tet3dp1 (pctet3d gr) |
| Create a tet3dp1 object using a tet3d mesh. More... | |
| void | del_tet3dp1 (ptet3dp1 dc) |
| Delete a tet3dp1 object. More... | |
| psparsematrix | build_tet3dp1_sparsematrix (pctet3dp1 dc) |
| Create a sparsematrix with a sparsity pattern matching the nodal basis functions. More... | |
| psparsematrix | build_tet3dp1_interaction_sparsematrix (pctet3dp1 dc) |
| Create a sparsematrix with a sparsity pattern matching the nodal basis functions. More... | |
| psparsematrix | build_tet3dp1_prolongation_sparsematrix (pctet3dp1 dfine, pctet3dp1 dcoarse, pctet3dref rf) |
| Create a prolongation matrix. More... | |
| void | assemble_tet3dp1_laplace_sparsematrix (pctet3dp1 dc, psparsematrix A, psparsematrix Af) |
| Assemble stiffness matrix. More... | |
| void | assemble_tet3dp1_mass_sparsematrix (pctet3dp1 dc, psparsematrix M, psparsematrix Mf) |
| Assemble mass matrix. More... | |
| void | assemble_tet3dp1_dirichlet_avector (pctet3dp1 dc, field(*f)(const real *x, void *fdata), void *fdata, pavector d) |
| Discretize Dirichlet boundary values. More... | |
| void | assemble_tet3dp1_functional_avector (pctet3dp1 dc, field(*f)(const real *x, void *fdata), void *fdata, pavector b) |
Discretize an  -functional. More... -functional. More... | |
| real | normmax_tet3dp1 (pctet3dp1 dc, field(*f)(const real *x, void *fdata), void *fdata, pavector xs) |
| Compute the vertex-wise maximum norm of the discretization error. More... | |
| real | norml2_tet3dp1 (pctet3dp1 dc, field(*f)(const real *x, void *fdata), void *fdata, pcavector xs, pcavector xf) |
Compute the  -norm of the discretization error. More... -norm of the discretization error. More... | |
| pclustergeometry | build_tet3dp1_clustergeometry (pctet3dp1 p1, uint *idx) |
| Create a clustergeometry object for a FEM-discretisation with p1-functions. More... | |
Piecewise linear space with nodal basis functions on a three-dimensional tetrahedral mesh.
| void assemble_tet3dp1_dirichlet_avector | ( | pctet3dp1 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pavector | d | ||
| ) |
Discretize Dirichlet boundary values.
For each fixed vertex, the function  is evaluated and the result is written to the corresponding entry in the result. In the standard case, this provides us with a coefficient vector corresponding to the piecewise linear interpolation of the Dirichlet boundary values. Subtracting
is evaluated and the result is written to the corresponding entry in the result. In the standard case, this provides us with a coefficient vector corresponding to the piecewise linear interpolation of the Dirichlet boundary values. Subtracting  from the right-hand side of our equation, where
from the right-hand side of our equation, where  is the interaction matrix, yields the right-hand side of the problem with homogeneous Dirichlet boundary conditions.
is the interaction matrix, yields the right-hand side of the problem with homogeneous Dirichlet boundary conditions.
| dc | tet3dp1 object describing the trial space. |
| f | Dirichlet boundary values. |
| fdata | Additional data for f. |
| d | Target vector of dimension dc->nfix. |
| void assemble_tet3dp1_functional_avector | ( | pctet3dp1 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pavector | b | ||
| ) |
Discretize an  -functional.
-functional.
For each triangle tetrahedra, the element vector is computed by applying the edge-midpoint quadrature. Its components are then added to the corresponding entries in 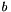 . Since
. Since 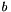 is cleared before this step, the result is given by
is cleared before this step, the result is given by  .
.
| dc | tet3dp1 object describing the trial space. |
| f | Right-hand side function. |
| fdata | Additional data for f. |
| b | Target vector of dimension dc->ndof. |
| void assemble_tet3dp1_laplace_sparsematrix | ( | pctet3dp1 | dc, |
| psparsematrix | A, | ||
| psparsematrix | Af | ||
| ) |
Assemble stiffness matrix.
Element matrices for all tetrahedra are computed and added to the corresponding entries in A and Af.
| dc | tet3dp1 object describing the trial space. |
| A | Target matrix for degrees of freedom. |
| Af | Target matrix for interactions between fixed vertices and degrees of freedom. |
| void assemble_tet3dp1_mass_sparsematrix | ( | pctet3dp1 | dc, |
| psparsematrix | M, | ||
| psparsematrix | Mf | ||
| ) |
Assemble mass matrix.
Element matrices for all tetrahedra are computed and added to the corresponding entries in M and Mf.
| dc | tet3dp1 object describing the trial space. |
| M | Target matrix for degrees of freedom. |
| Mf | Target matrix for interactions between fixed vertices and degrees of freedom. |
| pclustergeometry build_tet3dp1_clustergeometry | ( | pctet3dp1 | p1, |
| uint * | idx | ||
| ) |
Create a clustergeometry object for a FEM-discretisation with p1-functions.
Create a clustergeometry object basing on a tetrahedral tet3d mesh and linear nodal basis function.
| p1 | tet3dp1 object. |
| idx | Array of indices. |
| psparsematrix build_tet3dp1_interaction_sparsematrix | ( | pctet3dp1 | dc | ) |
Create a sparsematrix with a sparsity pattern matching the nodal basis functions.
Creates a sparse matrix matching the nodal basis functions: if the supports of basis functions  and
and  share at least one triangle, the entry
share at least one triangle, the entry 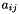 appears in the graph of the matrix.
appears in the graph of the matrix.
Here, only 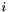 refers to a degree of freedom, while
refers to a degree of freedom, while  is the index of a fixed vertex, i.e., has to be between
is the index of a fixed vertex, i.e., has to be between 0 and nfix-1.
| dc | tet3dp1 object describing the space. |
dc->ndof rows and dc->nfix columns. | psparsematrix build_tet3dp1_prolongation_sparsematrix | ( | pctet3dp1 | dfine, |
| pctet3dp1 | dcoarse, | ||
| pctet3dref | rf | ||
| ) |
Create a prolongation matrix.
dcoarse and dfine have to correspond to a coarse mesh and its refinement created by refine_tet3d. The refinement relationship is described by rf.
This function not only creates the matrix, but also fills it with correct coefficients.
| dfine | tet3dp1 object corresponding to the refined mesh. |
| dcoarse | tet3dp1 object corresponding to the coarse mesh. |
| rf | Refinement relationship. |
| psparsematrix build_tet3dp1_sparsematrix | ( | pctet3dp1 | dc | ) |
Create a sparsematrix with a sparsity pattern matching the nodal basis functions.
Creates a sparse matrix matching the nodal basis functions: if the supports of basis functions  and
and  share at least one triangle, the entry
share at least one triangle, the entry 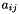 appears in the graph of the matrix.
appears in the graph of the matrix.
Here, both 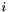 and
and  refer to degrees of freedom, i.e., there indices are between
refer to degrees of freedom, i.e., there indices are between 0 and ndof-1.
| dc | tet3dp1 object describing the space. |
dc->ndof rows and columns. | real norml2_tet3dp1 | ( | pctet3dp1 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pcavector | xs, | ||
| pcavector | xf | ||
| ) |
Compute the  -norm of the discretization error.
-norm of the discretization error.
Compare the function f to the discrete function described by the vector xs (for the degrees of freedom) and xf (for the fixed vertices). Measure the difference in the  -norm.
-norm.
| dc | tet3dp1 object describing the trial space. |
| f | Function. |
| fdata | Additional data for f. |
| xs | Coefficients of discrete function. |
| xf | Coefficients of fixed part of discrete function |
 -norm of discretization error.
-norm of discretization error. | real normmax_tet3dp1 | ( | pctet3dp1 | dc, |
| field(*)(const real *x, void *fdata) | f, | ||
| void * | fdata, | ||
| pavector | xs | ||
| ) |
Compute the vertex-wise maximum norm of the discretization error.
Evaluate f in all non-fixed vertices and compute the difference with the corresponding component of xs. The maximum of the absolute values gives the vertex-wise  -norm of the discretization error.
-norm of the discretization error.
| dc | tet3dp1 object describing the trial space. |
| f | Function. |
| fdata | Additional data for f. |
| xs | Coefficients of discrete function. |
 -norm of discretization error.
-norm of discretization error.  1.8.11
1.8.11