 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
Main container object for computation of BEM related matrices and vectors. More...
#include <bem3d.h>
Data Fields | |
| pcsurface3d | gr |
| Polyedric 3 dimensional surface mesh. More... | |
| psingquad2d | sq |
| Quadrature rules used within BEM computation. More... | |
| basisfunctionbem3d | row_basis |
| Type of basis function for neumann-data. | |
| basisfunctionbem3d | col_basis |
| Type of basis function for dirichlet-data. | |
| real * | mass |
| Mass-matrix of reference basis functions. More... | |
| field | alpha |
Boundary integral operator + 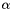 mass matrix. mass matrix. | |
| field | k |
| Wavenumber for Helmholtz type problems, possibly complex valued. | |
| field | kernel_const |
| A constant factor extracted from the kernel function to speed up quadrature. | |
| plistnode * | v2t |
| This field describes the mapping from the vertices of a geometry to the triangles they belong to. More... | |
| void(* | nearfield )(const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N) |
| Computes nearfield entries of Galerkin matrices. More... | |
| void(* | nearfield_far )(const uint *ridx, const uint *cidx, pcbem3d bem, bool ntrans, pamatrix N) |
| Computes nearfield entries of Galkerin matrices for disjoint clusters. More... | |
| void(* | farfield_rk )(pccluster rc, uint rname, pccluster cc, uint cname, pcbem3d bem, prkmatrix R) |
| Computes rank-k-approximations of a given block. More... | |
| void(* | farfield_u )(uint rname, uint cname, uint bname, pcbem3d bem) |
Computes coupling matrix  for uniform matrices. More... for uniform matrices. More... | |
| void(* | farfield_wave_u )(uint rname, uint cname, uint bname, pcbem3d bem) |
Computes coupling matrix  for duniform matrices for some direction for duniform matrices for some direction 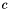 . More... . More... | |
| void(* | leaf_row )(uint rname, pcbem3d bem) |
Computes the the matrix  for a leaf cluster for a leaf cluster  . More... . More... | |
| void(* | leaf_wave_row )(uint rname, pcbem3d bem) |
Computes the the matrix  for a leaf cluster for a leaf cluster  and a direction and a direction  . More... . More... | |
| void(* | leaf_col )(uint cname, pcbem3d bem) |
Computes the the matrix  for a leaf cluster for a leaf cluster  . More... . More... | |
| void(* | leaf_wave_col )(uint cname, pcbem3d bem) |
Computes the the matrix  for a leaf cluster for a leaf cluster  and a direction and a direction  . More... . More... | |
| void(* | transfer_row )(uint rname, pcbem3d bem) |
Computes the transfer matrices  for a cluster for a cluster  . More... . More... | |
| void(* | transfer_wave_row )(uint rname, pcbem3d bem) |
Computes the transfer matrices  for a cluster for a cluster  and directions and directions  . The father cluster . The father cluster 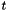 is using the wave-Lagrange basis while the sons is using the wave-Lagrange basis while the sons  use the standard Lagrange basis. More... use the standard Lagrange basis. More... | |
| void(* | transfer_wave_wave_row )(uint rname, pcbem3d bem) |
Computes the transfer matrices  for a cluster for a cluster  and directions and directions  . Both, the father cluster . Both, the father cluster 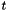 and sons and sons  are using the wave-Lagrange basis. More... are using the wave-Lagrange basis. More... | |
| void(* | transfer_col )(uint cname, pcbem3d bem) |
Computes the transfer matrices  for a cluster for a cluster  . More... . More... | |
| void(* | transfer_wave_col )(uint cname, pcbem3d bem) |
Computes the transfer matrices  for a cluster for a cluster  and directions and directions  . The father cluster . The father cluster 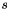 is using the wave-Lagrange basis while the sons is using the wave-Lagrange basis while the sons  use the standard Lagrange basis. More... use the standard Lagrange basis. More... | |
| void(* | transfer_wave_wave_col )(uint cname, pcbem3d bem) |
Computes the transfer matrices  for a cluster for a cluster  and directions and directions  . Both, the father cluster . Both, the father cluster 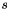 and sons and sons  are using the wave-Lagrange basis. More... are using the wave-Lagrange basis. More... | |
| paprxbem3d | aprx |
| A collection of necessary data structures for approximating matrices with various techniques. More... | |
| pparbem3d | par |
| Some helpers to make parallel computations possible. More... | |
| pkernelbem3d | kernels |
| A collection of callback functions for different types of kernel evaluations. More... | |
Main container object for computation of BEM related matrices and vectors.
This struct defines the essential part of all calculations concerning BEM. Just creating a simple bem3d object is not intended, though possible. Therefore call a problem specific constructor such as new_slp_laplace_bem3d or new_dlp_laplace_bem3d . This will initialize all needed callback functions to build up at least dense matrices. To be able to create h- or h2matrix approximations one needs to call one of the set_hmatrix_aprx* or set_h2matrix_aprx* depending on the type of your matrix, to fully initialize the bem3d object. Afterwards you can build up your desired matrix approximation with a few simple functions calls, delivered by the bem3d object, using your favored approximation technique. Calling another of these " set " functions will reinitialize the bem3d object and you can build another approximation with a different technique.
| paprxbem3d aprx |
A collection of necessary data structures for approximating matrices with various techniques.
Necessary Objects for approximation matrices with different approximation schemes are stored within aprx.
Computes rank-k-approximations of a given block.
This callback function computes a rank-k-approximation of a matrix block given by row cluster rc and column cluster cc. The Matrices A and B are stored in a rank-k-matrix R.
| rc | Current row cluster . |
| rname | Enumerated number of current row cluster rc. |
| cc | Current column cluster |
| cname | Enumerated number of current column cluster cc. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| R | Rank-k-matrix, which takes up the resulting matrices A and B . The rank k is defined by the underlying approximation technique. |
Computes coupling matrix  for uniform matrices.
for uniform matrices.
While using h2-matrices the coupling matrices  are computed by this callback function. Coupling matrices are stored in the struct uniform defining a certain block of the whole h2-matrix.
are computed by this callback function. Coupling matrices are stored in the struct uniform defining a certain block of the whole h2-matrix.
| rname | Enumerated number of current row cluster clusterbasis U->rb. |
| cname | Enumerated number of current column clusterbasis U->cb. |
| bmame | Enumerated number of current block. From that number an object of type uniform containing the coupling matrix  , the row clusterbasis , the row clusterbasis U->rb and the column clusterbasis U->cb can be derived. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
Computes coupling matrix  for duniform matrices for some direction
for duniform matrices for some direction 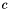 .
.
While using Dh2-matrices the coupling matrices  are computed by this callback function. Coupling matrices are stored in the struct duniform defining a certain block of the whole Dh2-matrix.
are computed by this callback function. Coupling matrices are stored in the struct duniform defining a certain block of the whole Dh2-matrix.
| rname | Enumerated number of current row dcluster dclusterbasis U->rb. |
| cname | Enumerated number of current column dclusterbasis U->cb. |
| bmame | Enumerated number of current dblock. From that number an object of type duniform containing the coupling matrix  , the row dclusterbasis , the row dclusterbasis U->rb and the column dclusterbasis U->cb can be derived. |
| bem | BEM-object containing additional information for computation of the matrix entries. |
| pcsurface3d gr |
Polyedric 3 dimensional surface mesh.
Polyedric boundary mesh used for the BEM-problem.
| pkernelbem3d kernels |
A collection of callback functions for different types of kernel evaluations.
This struct defines a set of callback functions that are based on the fundamental solution of the underlying problem. They are used to build up approximations that will be used within farfield_rk , farfield_u , leaf_row , leaf_col , transfer_row and transfer_col. In Order to receive correct result, the callback functions defined in kernels have to be set correctly to the given problem by a constructor. These callback functions also depend on the utilized basis functions for either neumann- and dirichlet-data. As an example the constructors new_slp_laplace_bem3d and new_dlp_laplace_bem3d should serve.
Computes the the matrix  for a leaf cluster
for a leaf cluster  .
.
leaf_col is used for building up a clusterbasis for the set  for h2matrices. For each
for h2matrices. For each  leaf_col will construct the matrix
leaf_col will construct the matrix  . In case of nested clusterbasis transfer_col has also to be set to a valid function constructing suitable transfer matrices
. In case of nested clusterbasis transfer_col has also to be set to a valid function constructing suitable transfer matrices  .
.
| bem | BEM-object containing additional information for computation of the matrix entries. |
| cname | Enumerated number of current column clusterbasis cb. |
Computes the the matrix  for a leaf cluster
for a leaf cluster  .
.
leaf_row is used for building up a clusterbasis for the set  for h2matrices. For each
for h2matrices. For each  leaf_row will construct the matrix
leaf_row will construct the matrix  . In case of nested clusterbasis transfer_row has also to be set to a valid function constructing suitable transfer matrices
. In case of nested clusterbasis transfer_row has also to be set to a valid function constructing suitable transfer matrices  .
.
| bem | BEM-object containing additional information for computation of the matrix entries. |
| rname | Enumerated number of current row clusterbasis rb. |
Computes the the matrix  for a leaf cluster
for a leaf cluster  and a direction
and a direction  .
.
leaf_wave_col is used for building up a dclusterbasis for the set  for Dh2matrices. For each
for Dh2matrices. For each  and for all directions
and for all directions  leaf_wave_col will construct the matrix
leaf_wave_col will construct the matrix  . In case of nested dclusterbasis transfer_wave_col and transfer_wave_wave_col also have to be set to valid functions constructing suitable transfer matrices
. In case of nested dclusterbasis transfer_wave_col and transfer_wave_wave_col also have to be set to valid functions constructing suitable transfer matrices  .
.
| bem | BEM-object containing additional information for computation of the matrix entries. |
| cname | Enumerated number of current column dclusterbasis cb. |
Computes the the matrix  for a leaf cluster
for a leaf cluster  and a direction
and a direction  .
.
leaf_wave_row is used for building up a dclusterbasis for the set  for Dh2matrices. For each
for Dh2matrices. For each  and all directions
and all directions  . leaf_wave_row will construct the matrix
. leaf_wave_row will construct the matrix  . In case of nested dclusterbasis transfer_wave_row and transfer_wave_wave_row also have to be set to valid functions constructing suitable transfer matrices
. In case of nested dclusterbasis transfer_wave_row and transfer_wave_wave_row also have to be set to valid functions constructing suitable transfer matrices  .
.
| bem | BEM-object containing additional information for computation of the matrix entries. |
| rname | Enumerated number of current row dclusterbasis rb. |
| real* mass |
Mass-matrix of reference basis functions.
Mass-matrix for all combinations of reference basis functions  and
and  . Entries are computed as:
. Entries are computed as:
![\[ M_{ij} = \int_\Gamma \widehat\varphi_i(x) \cdot \widehat\psi_j(x) \, \mathrm d x \]](../../form_247.png)
Computes nearfield entries of Galerkin matrices.
This callback function computes 'nearfield' entries of the underlying problem and integral-operator.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
Computes nearfield entries of Galkerin matrices for disjoint clusters.
This callback function computes 'nearfield' entries of the underlying problem and integral-operator.
| ridx | Defines the indices of row boundary elements used. If ridx equals NULL, then Elements 0, ..., N->rows-1 are used. |
| cidx | Defines the indices of column boundary elements used. If cidx equals NULL, then Elements 0, ..., N->cols-1 are used. |
| bem | Bem3d object, that contains additional Information for the computation of the matrix entries. |
| ntrans | Is a boolean flag to indicates the way of storing the entries in matrix N . If ntrans == true the matrix entries will be stored in a transposed way. |
| N | For ntrans == false the matrix entries are computed as:
|
| pparbem3d par |
Some helpers to make parallel computations possible.
For the sake of parallelism we need some auxiliary data structure, which are all collected within the struct par. Most commonly used is this struct for enumerated non linear data structures such als cluster- or blocktrees.
| psingquad2d sq |
Quadrature rules used within BEM computation.
Singular quadrature formulas used within boundary-integral-Operator computation.
Computes the transfer matrices  for a cluster
for a cluster  .
.
transfer_col will build up the transfer matrices  , for all
, for all  and
and  . For a cluster
. For a cluster  transfer_col will compute the matrices
transfer_col will compute the matrices  ,
,  . The matrix
. The matrix  is stored in
is stored in cb->son[0]->E,  is stored in
is stored in cb->son[1]->E,  is stored in
is stored in cb->son[ .  ]->E
]->E
| bem | BEM-object containing additional information for computation of the matrix entries. |
| cname | Enumerated number of current column clusterbasis cb. |
Computes the transfer matrices  for a cluster
for a cluster  .
.
transfer_row will build up the transfer matrices  , for all
, for all  and
and  . For a cluster
. For a cluster  transfer_row will compute the matrices
transfer_row will compute the matrices  ,
,  . The matrix
. The matrix  is stored in
is stored in rb->son[0]->E,  is stored in
is stored in rb->son[1]->E,  is stored in
is stored in rb->son[ .  ]->E
]->E
| bem | BEM-object containing additional information for computation of the matrix entries. |
| rname | Enumerated number of current row clusterbasis rb. |
Computes the transfer matrices  for a cluster
for a cluster  and directions
and directions  . The father cluster
. The father cluster 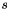 is using the wave-Lagrange basis while the sons
is using the wave-Lagrange basis while the sons  use the standard Lagrange basis.
use the standard Lagrange basis.
transfer_wave_col will build up the transfer matrices  , for all
, for all  and
and  and directions
and directions  . For a cluster
. For a cluster  transfer_wave_col will compute the matrices
transfer_wave_col will compute the matrices  ,
,  and
and  . The matrix
. The matrix  is stored in
is stored in cb->son[0]->E + 0,  is stored in
is stored in cb->son[0]->E + 1,  is stored in
is stored in cb->son[ .  ]->E + (d - 1)
]->E + (d - 1)
| bem | BEM-object containing additional information for computation of the matrix entries. |
| cname | Enumerated number of current column dclusterbasis cb. |
Computes the transfer matrices  for a cluster
for a cluster  and directions
and directions  . The father cluster
. The father cluster 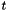 is using the wave-Lagrange basis while the sons
is using the wave-Lagrange basis while the sons  use the standard Lagrange basis.
use the standard Lagrange basis.
transfer_wave_row will build up the transfer matrices  , for all
, for all  and
and  and directions
and directions  . For a cluster
. For a cluster  transfer_wave_row will compute the matrices
transfer_wave_row will compute the matrices  ,
,  and
and  . The matrix
. The matrix  is stored in
is stored in rb->son[0]->E + 0,  is stored in
is stored in rb->son[0]->E + 1,  is stored in
is stored in rb->son[ .  ]->E + (d - 1)
]->E + (d - 1)
| bem | BEM-object containing additional information for computation of the matrix entries. |
| rname | Enumerated number of current row dclusterbasis rb. |
Computes the transfer matrices  for a cluster
for a cluster  and directions
and directions  . Both, the father cluster
. Both, the father cluster 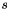 and sons
and sons  are using the wave-Lagrange basis.
are using the wave-Lagrange basis.
transfer_wave_wave_col will build up the transfer matrices  , for all
, for all  and
and  and directions
and directions  . For a cluster
. For a cluster  transfer_wave_wave_col will compute the matrices
transfer_wave_wave_col will compute the matrices  ,
,  and
and  . The matrix
. The matrix  is stored in
is stored in cb->son[0]->E + 0,  is stored in
is stored in cb->son[0]->E + 1,  is stored in
is stored in cb->son[ . The used directions  ]->E + (d - 1)
]->E + (d - 1) correspond to some difference between directions
correspond to some difference between directions  used for the father
used for the father 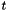 and directions
and directions  . Therefore it holds
. Therefore it holds
![\[ c_\iota = c^f_\iota - c^s_\iota = c^f_\iota - \operatorname{sondir}(c^f_\iota) \]](../../form_387.png)
| bem | BEM-object containing additional information for computation of the matrix entries. |
| cname | Enumerated number of current column dclusterbasis cb. |
Computes the transfer matrices  for a cluster
for a cluster  and directions
and directions  . Both, the father cluster
. Both, the father cluster 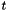 and sons
and sons  are using the wave-Lagrange basis.
are using the wave-Lagrange basis.
transfer_wave_wave_row will build up the transfer matrices  , for all
, for all  and
and  and directions
and directions  . For a cluster
. For a cluster  transfer_wave_wave_row will compute the matrices
transfer_wave_wave_row will compute the matrices  ,
,  and
and  . The matrix
. The matrix  is stored in
is stored in rb->son[0]->E + 0,  is stored in
is stored in rb->son[0]->E + 1,  is stored in
is stored in rb->son[ . The used directions  ]->E + (d - 1)
]->E + (d - 1) correspond to some difference between directions
correspond to some difference between directions  used for the father
used for the father 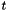 and directions
and directions  . Therefore it holds
. Therefore it holds
![\[ c_\iota = c^f_\iota - c^s_\iota = c^f_\iota - \operatorname{sondir}(c^f_\iota) \]](../../form_387.png)
| bem | BEM-object containing additional information for computation of the matrix entries. |
| rname | Enumerated number of current row dclusterbasis rb. |
| plistnode* v2t |
This field describes the mapping from the vertices of a geometry to the triangles they belong to.
The length of this array is equal to the number of vertices. For each vertex  the list
the list v2t[i] enumerates all triangles that share this vertex  .
.
This can be usefull within computation of matrix entries when linear basis functions are involved.
 1.8.11
1.8.11