 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
This module servers as a wrapper for all calls to BLAS and LAPACK routines. More...
Macros | |
| #define | h2_dot(n, x, incx, y, incy) zdotc_(n, x, incx, y, incy) |
Compute the dot product of two field vectors  and and  of length of length n. More... | |
| #define | h2_rdot(n, x, incx, y, incy) ddot_(n, x, incx, y, incy) |
Compute the dot product of two real vectors  and and  of length of length n. More... | |
| #define | h2_axpy(n, alpha, x, incx, y, incy) zaxpy_(n, alpha, x, incx, y, incy) |
Add a field vector  to another field vector to another field vector  . More... . More... | |
| #define | h2_raxpy(n, alpha, x, incx, y, incy) daxpy_(n, alpha, x, incx, y, incy) |
Add a real vector  to another field vector to another field vector  . More... . More... | |
| #define | h2_scal(n, alpha, x, incx) zscal_(n, alpha, x, incx) |
Scales a field vector  by a field scalar by a field scalar  . More... . More... | |
| #define | h2_rscal(n, alpha, x, incx) zdscal_(n, alpha, x, incx) |
Scales a field vector  by a real scalar by a real scalar  . More... . More... | |
| #define | h2_nrm2(n, x, incx) dznrm2_(n, x, incx) |
Computes the 2-norm  of a field vector of a field vector  . More... . More... | |
| #define | h2_swap(n, x, incx, y, incy) zswap_(n, x, incx, y, incy) |
Swaps to entries of two field vectors  and and  . More... . More... | |
| #define | h2_gemv(trans, m, n, alpha, a, lda, x, incx, beta, y, incy) zgemv_(trans, m, n, alpha, a, lda, x, incx, beta, y, incy) |
Compute matrix vector product of a general matrix  with input vector with input vector  and output vector and output vector 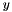 . More... . More... | |
| #define | h2_trmv(uplo, trans, diag, n, a, lda, x, incx) ztrmv_(uplo, trans, diag, n, a, lda, x, incx) |
Compute matrix vector product of a triangular matrix  with input and output vector with input and output vector  . More... . More... | |
| #define | h2_ger(m, n, alpha, x, incx, y, incy, a, lda) zgerc_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_gerc(m, n, alpha, x, incx, y, incy, a, lda) zgerc_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_geru(m, n, alpha, x, incx, y, incy, a, lda) zgeru_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_syr(uplo, n, alpha, x, incx, a, lda) zher_(uplo, n, alpha, x, incx, a, lda) |
Adds a symmetric/hermetian rank-1-update  to a matrix to a matrix  . More... . More... | |
| #define | h2_gemm(transa, transb, m, n, k, alpha, a, lda, b, ldb, beta, c, ldc) zgemm_(transa, transb, m, n, k, alpha, a, lda, b, ldb, beta, c, ldc) |
Compute matrix-matrix-multiplication for general matrices  and and  . More... . More... | |
| #define | h2_trmm(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) ztrmm_(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
Compute matrix-matrix-multiplication for triangular matrices  and a general matrix and a general matrix  . More... . More... | |
| #define | h2_trsm(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) ztrsm_(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
Solves a linear system of equations with a triangular matrix  and a right-hand-side matrix and a right-hand-side matrix  . More... . More... | |
| #define | h2_lacgv(n, x, incx) zlacgv_(n, x, incx) |
Conjugates a vector of field  . More... . More... | |
| #define | h2_potrf(uplo, n, a, lda, info) zpotrf_(uplo, n, a, lda, info) |
Computes the Cholesky factorization of symmetric/hermitian positive definite matrix  in-place. More... in-place. More... | |
| #define | h2_larf(side, m, n, v, incv, tau, c, ldc, work) zlarf_(side, m, n, v, incv, tau, c, ldc, work) |
Applies an elementary reflector  to a matrix to a matrix  . More... . More... | |
| #define | h2_larfg(n, alpha, x, incx, tau) zlarfg_(n, alpha, x, incx, tau) |
Create an elementary reflector  . More... . More... | |
| #define | h2_geqrf(m, n, a, lda, tau, work, lwork, info) zgeqrf_(m, n, a, lda, tau, work, lwork, info) |
Compute a QR-decomposition of the matrix  . More... . More... | |
| #define | h2_ormqr(side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info) zunmqr_(side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info) |
Apply orthogonal/unitary matrix  from "Left" or from "Right" to a matrix from "Left" or from "Right" to a matrix  . More... . More... | |
| #define | h2_orgqr(m, n, k, a, lda, tau, work, lwork, info) zungqr_(m, n, k, a, lda, tau, work, lwork, info) |
Generate the orthogonal/unitary matrix  out of its elementary reflectors out of its elementary reflectors  . More... . More... | |
| #define | h2_steqr(compz, n, d, e, z, ldz, work, info) zsteqr_(compz, n, d, e, z, ldz, work, info) |
Compute all eigenvalues and optionally all eigenvectors of a symmetric tridiagonal matrix  using implicit QL or QR method. More... using implicit QL or QR method. More... | |
| #define | h2_stev(jobz, n, d, e, z, ldz, work, info) dstev_(jobz, n, d, e, z, ldz, work, info) |
Compute all eigenvalues and optionally all eigenvectors of a real symmetric tridiagonal matrix  . More... . More... | |
| #define | h2_gesvd(jobu, jobvt, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, info) zgesvd_(jobu, jobvt, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, info) |
Compute the SVD of a general matrix  . More... . More... | |
| #define | h2_bdsqr(uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info) zbdsqr_(uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info) |
Compute the SVD of a real "Lower" or "Upper" bidiagonal matrix  . More... . More... | |
| #define | h2_heev(jobz, uplo, n, a, lda, w, work, lwork, rwork, info) zheev_(jobz, uplo, n, a, lda, w, work, lwork, rwork, info) |
Compute all eigenvalues and optionally all eigenvectors of a hermitian / symmetric matrix  . More... . More... | |
This module servers as a wrapper for all calls to BLAS and LAPACK routines.
For more detailed information about the imported functions, please refer e.g. to http://www.netlib.org/lapack/explore-html/index.html
| #define h2_axpy | ( | n, | |
| alpha, | |||
| x, | |||
| incx, | |||
| y, | |||
| incy | |||
| ) | zaxpy_(n, alpha, x, incx, y, incy) |
Add a field vector  to another field vector
to another field vector  .
.
| n | Length of both vectors x and y. |
| alpha | Field constant. |
| x | First field vector of length n. |
| incx | Stride for elements of x. |
| y | Second field vector of length n. |
| incy | Stride for elements of y. |
| #define h2_bdsqr | ( | uplo, | |
| n, | |||
| ncvt, | |||
| nru, | |||
| ncc, | |||
| d, | |||
| e, | |||
| vt, | |||
| ldvt, | |||
| u, | |||
| ldu, | |||
| c, | |||
| ldc, | |||
| rwork, | |||
| info | |||
| ) | zbdsqr_(uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info) |
Compute the SVD of a real "Lower" or "Upper" bidiagonal matrix  .
.
 is decomposed as
is decomposed as  .
.
If unitary matrices  ad
ad  that reduce a matrix
that reduce a matrix  to bidiagonal form, then the SVD of
to bidiagonal form, then the SVD of  is given by
is given by  .
.
Optionally the function may also compute  for some input matrix
for some input matrix  .
.
| uplo | Determines whether an "Upper" or a "Lower" bidiagonal matrix  is given. is given. |
| n | The order of the matrix  . . |
| ncvt | Number of columns of the matrix  . . |
| nru | Number of row of the matrix  . . |
| ncc | Number of columns of the matrix  . . |
| d | Real vector of length n containing the diagonal entries of  on entry and the singular values in descending order on exit. on entry and the singular values in descending order on exit. |
| e | Real vector of length n - 1 containing the offdiagonal entries of  . . |
| vt | Matrix of fields  on entry, on exit the matrix on entry, on exit the matrix  . . |
| ldvt | Leading dimension of the matrix  . . |
| u | Matrix of fields  on entry, on exit the matrix on entry, on exit the matrix  . . |
| ldu | Leading dimension of the matrix  . . |
| c | Matrix of fields  on entry, on exit the matrix on entry, on exit the matrix  . . |
| ldc | Leading dimension of the matrix  . . |
| rwork | Intermediate storage of size 2 n or max(1, 4*n - 4). |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_dot | ( | n, | |
| x, | |||
| incx, | |||
| y, | |||
| incy | |||
| ) | zdotc_(n, x, incx, y, incy) |
Compute the dot product of two field vectors  and
and  of length
of length n.
| n | Length of both vectors x and y. |
| x | First field vector of length n. |
| incx | Stride for elements of x. |
| y | Second field vector of length n. |
| incy | Stride for elements of y. |
x and y: 
| #define h2_gemm | ( | transa, | |
| transb, | |||
| m, | |||
| n, | |||
| k, | |||
| alpha, | |||
| a, | |||
| lda, | |||
| b, | |||
| ldb, | |||
| beta, | |||
| c, | |||
| ldc | |||
| ) | zgemm_(transa, transb, m, n, k, alpha, a, lda, b, ldb, beta, c, ldc) |
Compute matrix-matrix-multiplication for general matrices  and
and  .
.
Depending on the values of transa and transb one of the following operations is performed:  or
or  or
or  or
or  .
.
| transa | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| transb | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| m | Number of rows for the matrix a and matrix c. |
| n | Number of columns for the matrix b and the matrix c. |
| k | Number of columns for the matrix a and rows of the matrix b. |
| alpha | Field scalar value used in the above mentioned computation. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| b | The matrix  . . |
| ldb | Leading dimension of the matrix  |
| beta | Field scalar value used in the above mentioned computation. |
| c | The matrix  . . |
| ldc | Leading dimension of the matrix  |
| #define h2_gemv | ( | trans, | |
| m, | |||
| n, | |||
| alpha, | |||
| a, | |||
| lda, | |||
| x, | |||
| incx, | |||
| beta, | |||
| y, | |||
| incy | |||
| ) | zgemv_(trans, m, n, alpha, a, lda, x, incx, beta, y, incy) |
Compute matrix vector product of a general matrix  with input vector
with input vector  and output vector
and output vector 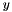 .
.
The operation  or
or  or
or  will be performed depending on the value of
will be performed depending on the value of trans and the current type of field.
| trans | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| m | Number of rows for the matrix a. |
| n | Number of columns for the matrix a. |
| alpha | Field scalar value used in the above mentioned computation. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| x | Input field vector  . Dimension of . Dimension of x should be at least n. |
| incx | Stride for elements of x. |
| beta | Field scalar value used in the above mentioned computation. |
| y | Output field vector  . Dimension of . Dimension of y should be at least m. |
| incy | Stride for elements of y. |
| #define h2_geqrf | ( | m, | |
| n, | |||
| a, | |||
| lda, | |||
| tau, | |||
| work, | |||
| lwork, | |||
| info | |||
| ) | zgeqrf_(m, n, a, lda, tau, work, lwork, info) |
Compute a QR-decomposition of the matrix  .
.
 will be factorized into an orthogonal/unitary matrix
will be factorized into an orthogonal/unitary matrix  and an upper triangular matrix
and an upper triangular matrix  .
.
Both matrices will be stored into the original matrix  and an additional vector of field
and an additional vector of field  .
.
| m | Rows of the matrix  . . |
| n | Columns of the matrix  . . |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| tau | Field vector containing the scaling factors for the elementary reflectors. |
| work | Intermediate storage of size lwork. |
| lwork | Size of the intermediate storage work. For a detailed description of this parameter, please refer to LAPACK documentation. |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_ger | ( | m, | |
| n, | |||
| alpha, | |||
| x, | |||
| incx, | |||
| y, | |||
| incy, | |||
| a, | |||
| lda | |||
| ) | zgerc_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix
to a matrix  .
.
The Computation  is performed.
is performed.
| m | Number of rows for the matrix a. |
| n | Number of columns for the matrix a. |
| alpha | Field scalar value used in the above mentioned computation. |
| x | First field vector  . Dimension of . Dimension of x should be m. |
| incx | Stride for elements of x. |
| y | Second field vector  . Dimension of . Dimension of y should be n. |
| incy | Stride for elements of y. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| #define h2_gerc | ( | m, | |
| n, | |||
| alpha, | |||
| x, | |||
| incx, | |||
| y, | |||
| incy, | |||
| a, | |||
| lda | |||
| ) | zgerc_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix
to a matrix  .
.
The Computation  is performed.
is performed.
| m | Number of rows for the matrix a. |
| n | Number of columns for the matrix a. |
| alpha | Field scalar value used in the above mentioned computation. |
| x | First field vector  . Dimension of . Dimension of x should be m. |
| incx | Stride for elements of x. |
| y | Second field vector  . Dimension of . Dimension of y should be n. |
| incy | Stride for elements of y. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| #define h2_geru | ( | m, | |
| n, | |||
| alpha, | |||
| x, | |||
| incx, | |||
| y, | |||
| incy, | |||
| a, | |||
| lda | |||
| ) | zgeru_(m, n, alpha, x, incx, y, incy, a, lda) |
Adds a rank-1-update  to a matrix
to a matrix  .
.
The Computation  is performed.
is performed.
| m | Number of rows for the matrix a. |
| n | Number of columns for the matrix a. |
| alpha | Field scalar value used in the above mentioned computation. |
| x | First field vector  . Dimension of . Dimension of x should be m. |
| incx | Stride for elements of x. |
| y | Second field vector  . Dimension of . Dimension of y should be n. |
| incy | Stride for elements of y. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| #define h2_gesvd | ( | jobu, | |
| jobvt, | |||
| m, | |||
| n, | |||
| a, | |||
| lda, | |||
| s, | |||
| u, | |||
| ldu, | |||
| vt, | |||
| ldvt, | |||
| work, | |||
| lwork, | |||
| rwork, | |||
| info | |||
| ) | zgesvd_(jobu, jobvt, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, info) |
Compute the SVD of a general matrix  .
.
 is decomposed as
is decomposed as  .
.
| jobu | If set to "All" all m columns of  are computed. are computed.If set to "Skinny" only the first min( m, n) columns of  are computed. are computed.If set to "Overwrite" only the first min( m, n) columns of  are computed and overwrite the entries of are computed and overwrite the entries of  . .If set to "No Vectors" no left singular vectors will be computed. |
| jobvt | If set to "All" all n columns of  are computed. are computed.If set to "Skinny" only the first min( m, n) columns of  are computed. are computed.If set to "Overwrite" only the first min( m, n) columns of  are computed and overwrite the entries of are computed and overwrite the entries of  . .If set to "No Vectors" no right singular vectors will be computed. |
| m | Number of rows of the matrix  . . |
| n | Number of rows of the matrix  . . |
| a | The matrix  . . |
| lda | Leading dimension of  . . |
| s | Vector of reals containing the singular vectors on exit. |
| u | Matrix containing the left singular vectors depending on the choice of jobu on exit. |
| ldu | Leading dimension of  . . |
| vt | Matrix containing the right singular vectors depending on the choice of jobvt on exit. |
| ldvt | Leading dimension of  . . |
| work | Intermediate storage of size lwork. |
| lwork | Size of the intermediate storage work. For a detailed description of this parameter, please refer to LAPACK documentation. |
| rwork | Intermediate storage of size 5*min(m, n). |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_heev | ( | jobz, | |
| uplo, | |||
| n, | |||
| a, | |||
| lda, | |||
| w, | |||
| work, | |||
| lwork, | |||
| rwork, | |||
| info | |||
| ) | zheev_(jobz, uplo, n, a, lda, w, work, lwork, rwork, info) |
Compute all eigenvalues and optionally all eigenvectors of a hermitian / symmetric matrix  .
.
| jobz | Is equal to "No Vectors" if only the eigenvalues should be computed and equal to "Vectors" if also eigenvectors should be computed. |
| uplo | Determines whether the lower triangular or the upper triangular part of the matrix  should be used. The value "Lower" refers to the first and the value "Upper" refers to the latter case. should be used. The value "Lower" refers to the first and the value "Upper" refers to the latter case. |
| n | Number of rows and columns of the matrix  . . |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| w | On exit the field vector 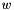 contains the eigenvalues in ascending order. contains the eigenvalues in ascending order. |
| work | Intermediate storage of size lwork. |
| lwork | Size of the intermediate storage work. For a detailed description of this parameter, please refer to LAPACK documentation. |
| rwork | Intermediate storage of size max(1, 3*n-2). |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_lacgv | ( | n, | |
| x, | |||
| incx | |||
| ) | zlacgv_(n, x, incx) |
Conjugates a vector of field  .
.
 .
.
| n | Length of the vector  . . |
| x | Field vector  . . |
| incx | Stride for elements of x. |
| #define h2_larf | ( | side, | |
| m, | |||
| n, | |||
| v, | |||
| incv, | |||
| tau, | |||
| c, | |||
| ldc, | |||
| work | |||
| ) | zlarf_(side, m, n, v, incv, tau, c, ldc, work) |
Applies an elementary reflector  to a matrix
to a matrix  .
.
Depending on the value of side either  or
or  is being performed.
is being performed.
| side | Determines if the matrix  should be multiplied from "Left" or from "Right" to the matrix should be multiplied from "Left" or from "Right" to the matrix  . . |
| m | Number of rows for the matrix  . . |
| n | Number of columns for the matrix  . . |
| v | Vector of fields  representing the matrix representing the matrix  . . |
| incv | Stride for the vector v. |
| tau | Field scalar value used in the above mentioned computation of  . . |
| c | The matrix  . . |
| ldc | Leading dimension of the matrix  |
| work | Intermediate storage of size n if side is equal to "Left" or of size m if side is equal to "Right". |
| #define h2_larfg | ( | n, | |
| alpha, | |||
| x, | |||
| incx, | |||
| tau | |||
| ) | zlarfg_(n, alpha, x, incx, tau) |
Create an elementary reflector  .
.
The properties of  are defined as
are defined as
![\[\bar H^T \begin{pmatrix} \alpha \\ \vec x \end{pmatrix} = \begin{pmatrix} \beta \\ \vec 0 \end{pmatrix}, \qquad \bar H^T H = I. \]](../../form_459.png)
 will be computed as
will be computed as
![\[H = I - \tau \begin{pmatrix} 1 \\ \vec v \end{pmatrix} \begin{pmatrix} 1 & \bar \vec v^T \end{pmatrix}. \]](../../form_460.png)
| n | Dimension of the elementary reflector. |
| alpha | On entry the scalar field value  , on exit the scalar field value , on exit the scalar field value  . . |
| x | On entry the field vector  , on exit the field vector , on exit the field vector  . . |
| incx | Stride for the vector x. |
| tau | The field scalar  . . |
| #define h2_nrm2 | ( | n, | |
| x, | |||
| incx | |||
| ) | dznrm2_(n, x, incx) |
Computes the 2-norm  of a field vector
of a field vector  .
.
| n | Length of vector x. |
| x | Field vector of length n. |
| incx | Stride for elements of x. |
 .
. | #define h2_orgqr | ( | m, | |
| n, | |||
| k, | |||
| a, | |||
| lda, | |||
| tau, | |||
| work, | |||
| lwork, | |||
| info | |||
| ) | zungqr_(m, n, k, a, lda, tau, work, lwork, info) |
Generate the orthogonal/unitary matrix  out of its elementary reflectors
out of its elementary reflectors  .
.
The matrix  will overwrite the matrix
will overwrite the matrix  on exit.
on exit.
| m | Number of rows for the matrix C. |
| n | Number of columns for the matrix C. |
| k | Number of elementary reflectors. |
| a | Matrix that contains the elementary reflectors of  as returned by h2_geqrf on entry and will contain the matrix as returned by h2_geqrf on entry and will contain the matrix  at exit. at exit. |
| lda | Leading dimension of the matrix  |
| tau | Field vector that contains the scaling factors of the elementary reflectors. |
| work | Intermediate storage of size lwork. |
| lwork | Size of the intermediate storage work. For a detailed description of this parameter, please refer to LAPACK documentation. |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_ormqr | ( | side, | |
| trans, | |||
| m, | |||
| n, | |||
| k, | |||
| a, | |||
| lda, | |||
| tau, | |||
| c, | |||
| ldc, | |||
| work, | |||
| lwork, | |||
| info | |||
| ) | zunmqr_(side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info) |
Apply orthogonal/unitary matrix  from "Left" or from "Right" to a matrix
from "Left" or from "Right" to a matrix  .
.
Depending on the values of side and trans one of the following operations is performed:  or
or  or
or  or
or  .
.
 is represented as product of elementary reflectors
is represented as product of elementary reflectors  .
.
| side | Determines if the matrix  should be multiplied from "Left" or from "Right" to the matrix should be multiplied from "Left" or from "Right" to the matrix  . . |
| trans | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| m | Number of rows for the matrix C. |
| n | Number of columns for the matrix C. |
| k | Number of elementary reflectors. |
| a | Matrix that contains the elementary reflectors of  as returned by h2_geqrf. as returned by h2_geqrf. |
| lda | Leading dimension of the matrix  |
| tau | Field vector that contains the scaling factors of the elementary reflectors. |
| c | Matrix  that will be overwritten by the above mentioned computation. that will be overwritten by the above mentioned computation. |
| ldc | Leading dimension of the matrix  |
| work | Intermediate storage of size lwork. |
| lwork | Size of the intermediate storage work. For a detailed description of this parameter, please refer to LAPACK documentation. |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_potrf | ( | uplo, | |
| n, | |||
| a, | |||
| lda, | |||
| info | |||
| ) | zpotrf_(uplo, n, a, lda, info) |
Computes the Cholesky factorization of symmetric/hermitian positive definite matrix  in-place.
in-place.
The matrix a gets partially overwritten by either a lower triangular matrix  if
if uplo is set to "Lower" or by an upper triangular matrix  , if
, if uplo is set to "Upper". In either cases it holds  or
or  .
.
| uplo | Determines whether the lower triangular matrix  or the upper triangular matrix or the upper triangular matrix  should be stored in the matrix should be stored in the matrix a. The value "Lower" refers to the first and the value "Upper" refers to the latter case. |
| n | Number of rows and columns of the matrix  . . |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_raxpy | ( | n, | |
| alpha, | |||
| x, | |||
| incx, | |||
| y, | |||
| incy | |||
| ) | daxpy_(n, alpha, x, incx, y, incy) |
Add a real vector  to another field vector
to another field vector  .
.
| n | Length of both vectors x and y. |
| alpha | Real constant. |
| x | First real vector of length n. |
| incx | Stride for elements of x. |
| y | Second real vector of length n. |
| incy | Stride for elements of y. |
| #define h2_rdot | ( | n, | |
| x, | |||
| incx, | |||
| y, | |||
| incy | |||
| ) | ddot_(n, x, incx, y, incy) |
Compute the dot product of two real vectors  and
and  of length
of length n.
| n | Length of both vectors x and y. |
| x | First real vector of length n. |
| incx | Stride for elements of x. |
| y | Second real vector of length n. |
| incy | Stride for elements of y. |
x and y: 
| #define h2_rscal | ( | n, | |
| alpha, | |||
| x, | |||
| incx | |||
| ) | zdscal_(n, alpha, x, incx) |
Scales a field vector  by a real scalar
by a real scalar  .
.
| n | Length of vector x. |
| alpha | Real constant. |
| x | Field vector of length n. |
| incx | Stride for elements of x. |
| #define h2_scal | ( | n, | |
| alpha, | |||
| x, | |||
| incx | |||
| ) | zscal_(n, alpha, x, incx) |
Scales a field vector  by a field scalar
by a field scalar  .
.
| n | Length of vector x. |
| alpha | Field constant. |
| x | Field vector of length n. |
| incx | Stride for elements of x. |
| #define h2_steqr | ( | compz, | |
| n, | |||
| d, | |||
| e, | |||
| z, | |||
| ldz, | |||
| work, | |||
| info | |||
| ) | zsteqr_(compz, n, d, e, z, ldz, work, info) |
Compute all eigenvalues and optionally all eigenvectors of a symmetric tridiagonal matrix  using implicit QL or QR method.
using implicit QL or QR method.
| compz | Is equal to "No Vectors" if only the eigenvalues should be computed and equal to "Vectors" if also eigenvectors should be computed. Otherwise compz should be equal to "Identity" if  was initialized by an identity matrix and both eigenvalues and eigenvectors should be computed. was initialized by an identity matrix and both eigenvalues and eigenvectors should be computed. |
| n | Order of the matrix  . . |
| d | Coefficients for the diagonal of  . . |
| e | Coefficients for the subdiagonals of  . . |
| z | If Eigenvectors should be computed, the columns of the matrix  will contain them at exit. will contain them at exit. |
| ldz | Leading dimension of the matrix  . . |
| work | Intermediate storage of size lwork. |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_stev | ( | jobz, | |
| n, | |||
| d, | |||
| e, | |||
| z, | |||
| ldz, | |||
| work, | |||
| info | |||
| ) | dstev_(jobz, n, d, e, z, ldz, work, info) |
Compute all eigenvalues and optionally all eigenvectors of a real symmetric tridiagonal matrix  .
.
| jobz | Is equal to "No Vectors" if only the eigenvalues should be computed and equal to "Vectors" if also eigenvectors should be computed. |
| n | Order of the matrix  . . |
| d | Coefficients for the diagonal of  . . |
| e | Coefficients for the subdiagonals of  . . |
| z | If Eigenvectors should be computed, the columns of the matrix  will contain them at exit. will contain them at exit. |
| ldz | Leading dimension of the matrix  . . |
| work | Intermediate storage of size lwork. |
| info | Return value for the computation. Equals zero if everything worked fine, otherwise a return code that indicates the problem is returned. |
| #define h2_swap | ( | n, | |
| x, | |||
| incx, | |||
| y, | |||
| incy | |||
| ) | zswap_(n, x, incx, y, incy) |
Swaps to entries of two field vectors  and
and  .
.
| n | Length of both vectors x and y. |
| x | First field vector of length n. |
| incx | Stride for elements of x. |
| y | Second field vector of length n. |
| incy | Stride for elements of y. |
| #define h2_syr | ( | uplo, | |
| n, | |||
| alpha, | |||
| x, | |||
| incx, | |||
| a, | |||
| lda | |||
| ) | zher_(uplo, n, alpha, x, incx, a, lda) |
Adds a symmetric/hermetian rank-1-update  to a matrix
to a matrix  .
.
The Computation  is performed.
is performed.
| uplo | Determines if an "upper" right or a "lower" left triangular matrix  should be used. should be used. |
| n | Number of rows and columns for the matrix a. |
| alpha | Field scalar value used in the above mentioned computation. |
| x | First field vector  . Dimension of . Dimension of x should be m. |
| incx | Stride for elements of x. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| #define h2_trmm | ( | side, | |
| uplo, | |||
| transa, | |||
| diag, | |||
| m, | |||
| n, | |||
| alpha, | |||
| a, | |||
| lda, | |||
| b, | |||
| ldb | |||
| ) | ztrmm_(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
Compute matrix-matrix-multiplication for triangular matrices  and a general matrix
and a general matrix  .
.
Depending on the values of transa and side one of the following operations is performed:  or
or  or
or  or
or  .
.
The operation is performed in-place, i.e. matrix  will be overwritten by the product of the both matrices.
will be overwritten by the product of the both matrices.
| side | Determines if the matrix  should be multiplied from "Left" or from "Right" to the matrix should be multiplied from "Left" or from "Right" to the matrix  . . |
| uplo | Determines if an "upper" right or a "lower" left triangular matrix  should be used. should be used. |
| transa | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| diag | Determines if a "Unit" diagonal should be used or "Non-unit" matrix coefficients stored within the matrix  . . |
| m | Number of rows for the matrix b. |
| n | Number of columns for the matrix b. |
| alpha | Field scalar value used in the above mentioned computation. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| b | The matrix  . . |
| ldb | Leading dimension of the matrix  |
| #define h2_trmv | ( | uplo, | |
| trans, | |||
| diag, | |||
| n, | |||
| a, | |||
| lda, | |||
| x, | |||
| incx | |||
| ) | ztrmv_(uplo, trans, diag, n, a, lda, x, incx) |
Compute matrix vector product of a triangular matrix  with input and output vector
with input and output vector  .
.
The operation  or
or  or
or  will be performed depending on the value of
will be performed depending on the value of trans and the current type of field.
| uplo | Determines if an "upper" right or a "lower" left triangular matrix  should be used. should be used. |
| trans | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| diag | Determines if a "Unit" diagonal should be used or "Non-unit" matrix coefficients stored within the matrix  . . |
| n | Number of row and columns for the matrix a. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| x | Input/output field vector  . Dimension of . Dimension of x should be at least n. |
| incx | Stride for elements of x. |
| #define h2_trsm | ( | side, | |
| uplo, | |||
| transa, | |||
| diag, | |||
| m, | |||
| n, | |||
| alpha, | |||
| a, | |||
| lda, | |||
| b, | |||
| ldb | |||
| ) | ztrsm_(side, uplo, transa, diag, m, n, alpha, a, lda, b, ldb) |
Solves a linear system of equations with a triangular matrix  and a right-hand-side matrix
and a right-hand-side matrix  .
.
Depending on the values of side and transa one of the following systems is being solved for a right-hand-side  in-place:
in-place:
 or
or  or
or  or
or  .
.
| side | Determines if the matrix  should be multiplied from "Left" or from "Right" to the matrix should be multiplied from "Left" or from "Right" to the matrix  . . |
| uplo | Determines if an "upper" right or a "lower" left triangular matrix  should be used. should be used. |
| transa | If set to "Conjugate transposed"  will be used. will be used.If set to "Transposed"  will be used. will be used.In all other cases  will be used for the computation. will be used for the computation. |
| diag | Determines if a "Unit" diagonal should be used or "Non-unit" matrix coefficients stored within the matrix  . . |
| m | Number of rows for the matrix b. |
| n | Number of columns for the matrix b. |
| alpha | Field scalar value used in the above mentioned computation. |
| a | The matrix  . . |
| lda | Leading dimension of the matrix  |
| b | The matrix  . . |
| ldb | Leading dimension of the matrix  |
 1.8.11
1.8.11