 |
H2Lib
3.0
|
 |
H2Lib
3.0
|
Algebraic operations with  -matrices.
More...
-matrices.
More...
Algebraic operations with  -matrices.
-matrices.
| void add_hmatrix_h2matrix | ( | pchmatrix | a, |
| ph2matrix | B, | ||
| pclusteroperator | rwf, | ||
| pclusteroperator | cwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
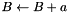
| a | : constant hmatrix |
| B | : overwritten by  |
| rwf | : has to be the father of the weights of the row clusterbasis of B, e.g. initialized by prepare_row_clusteroperator |
| cwf | : has to be the father of the weights of the col clusterbasis of B, e.g. initialized by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| void addmul_h2matrix | ( | field | alpha, |
| pch2matrix | a, | ||
| bool | btrans, | ||
| pch2matrix | B, | ||
| ph2matrix | C, | ||
| pclusteroperator | rwf, | ||
| pclusteroperator | cwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
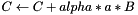
| alpha | : field |
| a | : constant h2matrix |
| btrans | : set if B has to be transposed |
| B | : constant h2matrix |
| C | : overwritten by  |
| rwf | : has to be the father of the weights of the row clusterbasis of C, e.g. initialised by prepare_row_clusteroperator |
| cwf | : has to be the father of the weights of the col clusterbasis of C, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| ph2matrix build_from_block_lower_h2matrix | ( | pcblock | b, |
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
builds a lower triangular H2-matrix based on block tree b

| b | : gives the block structure |
| rb | : the row cluster basis of the new h2matrix |
| cb | : the column cluster basis of the new h2matrix |
| ph2matrix build_from_block_upper_h2matrix | ( | pcblock | b, |
| pclusterbasis | rb, | ||
| pclusterbasis | cb | ||
| ) |
builds a upper triangular H2-matrix based on block tree b

| b | : gives the block structure |
| rb | : the row cluster basis of the new h2matrix |
| cb | : the column cluster basis of the new h2matrix |
| void choldecomp_h2matrix | ( | ph2matrix | a, |
| pclusteroperator | arwf, | ||
| pclusteroperator | acwf, | ||
| ph2matrix | L, | ||
| pclusteroperator | lrwf, | ||
| pclusteroperator | lcwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes the Cholesky decomposition 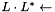 of a and stores the result in L and R
of a and stores the result in L and R
| a | : original matrix, overwritten by auxilliary results, e.g. initialised by init_cholesky_h2matrix |
| arwf | : has to be the father of the weights of the row clusterbasis of a, e.g. initialised by init_cholesky_h2matrix |
| acwf | : has to be the father of the weights of the column clusterbasis of a, e.g. initialised by init_cholesky_h2matrix |
| L | : cleared (lower) H2-matrix, has to have the same block tree structure as a, e.g. initialised by build_fromcluster_clusterbasis and build_from_block_lower_h2matrix |
| lrwf | : has to be the father of the weights of the row clusterbasis of L, e.g. initialised by prepare_row_clusteroperator |
| lcwf | : has to be the father of the weights of the column clusterbasis of L, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| void cholsolve_h2matrix_avector | ( | pch2matrix | a, |
| pavector | x | ||
| ) |

| a | : L is the lower triangular part of a with non-unit diagonal |
| x | : overwritten by  |
| pamatrix convert_h2matrix_amatrix | ( | bool | atrans, |
| pch2matrix | a | ||
| ) |
converts an h2matrix to a new amatrix

| atrans | : set if a has to be transposed |
| a | : constant h2matrix |
| phmatrix convert_h2matrix_hmatrix | ( | pch2matrix | a | ) |
converts an h2matrix to a new hmatrix
 ,
, | a | constant h2matrix |
converts an uniform matrix 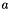 to a new rkmatrix
to a new rkmatrix
uses fastaddmul_clusterbasis_amatrix

| atrans | set if 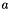 has to be transposed, i.e. has to be transposed, i.e.  |
| a | constant h2matrix |
| void init_cholesky_h2matrix | ( | ph2matrix | a, |
| pclusteroperator* | prwf, | ||
| pclusteroperator* | pcwf, | ||
| ptruncmode | tm | ||
| ) |
initialises a, rwf and cwf for choldecomp_h2matrix
| a | : upper diagonal blocks are set to  |
| prwf | : *prwf is initialised by prepare_row_clusteroperator for new a |
| pcwf | : *pcwf is initialised by prepare_col_clusteroperator for new a |
| tm | : used in prepare_row/col_clusteroperator |
| void invert_h2matrix | ( | ph2matrix | a, |
| pclusteroperator | arwf, | ||
| pclusteroperator | acwf, | ||
| ph2matrix | B, | ||
| pclusteroperator | brwf, | ||
| pclusteroperator | bcwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
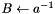
| a | : original matrix, overwritten by auxilliary results |
| arwf | : has to be the father of the weights of the row clusterbasis of a, e.g. initialised by prepare_row_clusteroperator |
| acwf | : has to be the father of the weights of the col clusterbasis of a, e.g. initialised by prepare_col_clusteroperator |
| B | : has to have zero entries and the same block tree structure as a, e.g. initialised by build_fromcluster_clusterbasis, buildfromblock_h2matrix and clear_h2matrix |
| brwf | : has to be the father of the weights of the row clusterbasis of B, e.g. initialised by prepare_row_clusteroperator |
| bcwf | : has to be the father of the weights of the col clusterbasis of B, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| void lowersolve_amatrix_h2matrix | ( | bool | aunit, |
| bool | atrans, | ||
| pcamatrix | a, | ||
| bool | xytrans, | ||
| pch2matrix | X, | ||
| ph2matrix | Y, | ||
| pclusteroperator | rwf, | ||
| pclusteroperator | cwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes 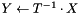 or
or 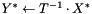 , using forward substitution
, using forward substitution
| aunit | : set if T has unit diagonal |
| atrans | : set if T is the transposed upper triangular part of a, else T is the lower triangular part of a |
| a | : constant amatrix |
| xytrans | : set if X and Y has to be transposed |
| X | : constant h2matrix |
| Y | : overwritten by  or or  |
| rwf | : has to be the father of the weights of the row clusterbasis of Y, e.g. initialised by prepare_row_clusteroperator |
| cwf | : has to be the father of the weights of the col clusterbasis of Y, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| void lowersolve_h2matrix | ( | bool | aunit, |
| bool | atrans, | ||
| pch2matrix | a, | ||
| bool | xytrans, | ||
| ph2matrix | X, | ||
| pclusteroperator | xrwf, | ||
| pclusteroperator | xcwf, | ||
| ph2matrix | Y, | ||
| pclusteroperator | yrwf, | ||
| pclusteroperator | ycwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes 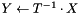 or
or 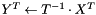 , using forward substitution
, using forward substitution
| aunit | : set if T has unit diagonal |
| atrans | : set if T is the transposed upper triangular part of a, else T is the lower triangular part of a |
| a | : constant h2matrix |
| xytrans | : set if X and Y has to be transposed |
| X | : overwritten by auxilliary results |
| xrwf | : has to be the father of the weights of the row clusterbasis of X, e.g. initialised by prepare_row_clusteroperator |
| xcwf | : has to be the father of the weights of the col clusterbasis of X, e.g. initialised by prepare_col_clusteroperator |
| Y | : overwritten by  or or  |
| yrwf | : has to be the father of the weights of the row clusterbasis of R, e.g. initialised by prepare_row_clusteroperator |
| ycwf | : has to be the father of the weights of the col clusterbasis of R, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| void lowersolve_h2matrix_amatrix | ( | bool | unit, |
| bool | atrans, | ||
| pch2matrix | a, | ||
| bool | xtrans, | ||
| pamatrix | X | ||
| ) |
computes 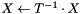 or
or 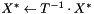 , using forward substitution
, using forward substitution
| unit | : set if T has unit diagonal |
| atrans | : set if T is the transposed upper triangular part of a, else T is the lower triangular part of a |
| a | : constant h2matrix |
| xtrans | : set if X has to be transposed |
| X | : overwritten by  or or  |
| void lowersolve_h2matrix_avector | ( | bool | unit, |
| bool | atrans, | ||
| pch2matrix | a, | ||
| pavector | x | ||
| ) |
computes 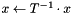 , using forward substitution
, using forward substitution
| unit | : set if T has unit diagonal |
| a | : constant h2matrix |
| atrans | : set if T is the transposed upper triangular part of a, else T is the lower triangular part of a |
| x | : overwritten by  |
| void lrdecomp_h2matrix | ( | ph2matrix | a, |
| pclusteroperator | arwf, | ||
| pclusteroperator | acwf, | ||
| ph2matrix | L, | ||
| pclusteroperator | lrwf, | ||
| pclusteroperator | lcwf, | ||
| ph2matrix | R, | ||
| pclusteroperator | rrwf, | ||
| pclusteroperator | rcwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes the LR-decomposition 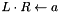 of a, L has unit diagonal
of a, L has unit diagonal
| a | : original matrix, overwritten by auxilliary results |
| arwf | : has to be the father of the weights of the row clusterbasis of a, e.g. initialised by prepare_row_clusteroperator |
| acwf | : has to be the father of the weights of the column clusterbasis of a, e.g. initialised by prepare_col_clusteroperator |
| L | : cleared (lower) H2-matrix, has to have the same block tree structure as a, e.g. initialised by build_fromcluster_clusterbasis and build_from_block_lower_h2matrix |
| lrwf | : has to be the father of the weights of the row clusterbasis of L, e.g. initialised by prepare_row_clusteroperator |
| lcwf | : has to be the father of the weights of the column clusterbasis of L, e.g. initialised by prepare_col_clusteroperator |
| R | : cleared (upper) H2-matrix, has to have the same block tree structure as a, e.g. initialised by build_fromcluster_clusterbasis and build_from_block_upper_h2matrix |
| rrwf | : has to be the father of the weights of the row clusterbasis of L, e.g. initialised by prepare_row_clusteroperator |
| rcwf | : has to be the father of the weights of the column clusterbasis of R, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| void lrsolve_h2matrix_avector | ( | pch2matrix | L, |
| pch2matrix | R, | ||
| pavector | x | ||
| ) |
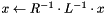
| L | : L is the lower triangular part with unit diagonal |
| R | R is the upper triangular part. |
| x | : overwritten by  |
| ph2matrix mul_h2matrix | ( | field | alpha, |
| ph2matrix | a, | ||
| ph2matrix | B, | ||
| ph2matrix | h2, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes 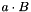 and converts it to a new h2matrix
and converts it to a new h2matrix

| alpha | : field |
| a | : constant h2matrix |
| B | : constant h2matrix |
| h2 | : the new h2matrix has the block structure as h2 |
| tm | : options of truncation |
| tol | : tolerance of truncation |
| prkmatrix mul_h2matrix_rkmatrix | ( | pch2matrix | a, |
| bool | btrans, | ||
| pch2matrix | B, | ||
| real | tol | ||
| ) |
computes 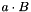 and converts it to a new rkmatrix
and converts it to a new rkmatrix

| a | : constant h2matrix |
| btrans | : set if B has to be transposed |
| B | : constant h2matrix |
| tol | : tolerance of truncation |
| void tolower_h2matrix | ( | ph2matrix | a | ) |
Clears all upper diagonal blocks of a h2matrix.
| a | h2matrix. |
| void uppersolve_amatrix_h2matrix | ( | bool | aunit, |
| bool | atrans, | ||
| pcamatrix | a, | ||
| bool | ytrans, | ||
| ph2matrix | Y, | ||
| pclusteroperator | rwf, | ||
| pclusteroperator | cwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes 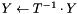 or
or 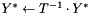 , using backward substitution
, using backward substitution
| aunit | : set if T has unit diagonal |
| atrans | : set if T is the transposed lower triangular part of a, else T is the upper triangular part of a |
| a | : constant amatrix |
| ytrans | : set if Y has to be transposed |
| Y | : overwritten by  or or  |
| rwf | : has to be the father of the weights of the row clusterbasis of Y, e.g. initialised by prepare_row_clusteroperator |
| cwf | : has to be the father of the weights of the col clusterbasis of Y, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
not tested yet
((atrans == false) && (xytrans == true)) is not implemented yet
((atrans == true) && (xytrans == false)) is not implemented yet
| void uppersolve_h2matrix | ( | bool | aunit, |
| bool | atrans, | ||
| pch2matrix | a, | ||
| bool | ytrans, | ||
| ph2matrix | Y, | ||
| pclusteroperator | yrwf, | ||
| pclusteroperator | ycwf, | ||
| ptruncmode | tm, | ||
| real | tol | ||
| ) |
computes 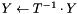 or
or 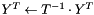 , using backward substitution
, using backward substitution
| aunit | : set if T has unit diagonal |
| atrans | : set if T is the transposed lower triangular part of a, else T is the upper triangular part of a |
| a | : constant h2matrix |
| ytrans | : set if Y has to be transposed |
| Y | : overwritten by  or or  |
| yrwf | : has to be the father of the weights of the row clusterbasis of R, e.g. initialised by prepare_row_clusteroperator |
| ycwf | : has to be the father of the weights of the col clusterbasis of R, e.g. initialised by prepare_col_clusteroperator |
| tm | : options of truncation |
| tol | : tolerance of truncation |
not tested yet
((atrans == true) && (xytrans == false)) is not implemented yet
| void uppersolve_h2matrix_amatrix | ( | bool | unit, |
| bool | atrans, | ||
| pch2matrix | a, | ||
| bool | xtrans, | ||
| pamatrix | X | ||
| ) |
computes 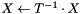 or
or 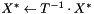 , using backward substitution
, using backward substitution
| unit | : set if T has unit diagonal |
| atrans | : set if T is the transposed lower triangular part of a, else T is the upper triangular part of a |
| a | : constant h2matrix |
| xtrans | : set if X has to be transposed |
| X | : overwritten by  |
| void uppersolve_h2matrix_avector | ( | bool | unit, |
| bool | atrans, | ||
| pch2matrix | a, | ||
| pavector | x | ||
| ) |
computes 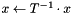 , using backward substitution
, using backward substitution
| unit | : set if T has unit diagonal |
| a | : constant h2matrix |
| atrans | : set if T is the transposed lower triangular part of a, else T is the upper triangular part of a |
| x | : overwritten by  |
 1.8.11
1.8.11