This module contains functions to setup and solve boundary integral equations for the Laplace operator in 2D. More...

Functions
pbem2d	new_slp_laplace_bem2d (pccurve2d gr, uint q, basisfunctionbem2d basis)
	Creates a new bem2d-object for computation of single layer potential matrix. More...

pbem2d	new_dlp_laplace_bem2d (pccurve2d gr, uint q, basisfunctionbem2d basis_neumann, basisfunctionbem2d basis_dirichlet, field alpha)
	Creates a new bem2d-object for computation of double layer potential matrix. More...

field	eval_dirichlet_linear_laplacebem2d (const real x, const real n)
	A simple linear harmonic function that will serve as dirichlet values. More...

field	eval_neumann_linear_laplacebem2d (const real x, const real n)
	A simple linear harmonic function that will serve as neumann values. More...

field	eval_dirichlet_quadratic_laplacebem2d (const real x, const real n)
	A simple quadratic harmonic function that will serve as dirichlet values. More...

field	eval_neumann_quadratic_laplacebem2d (const real x, const real n)
	A simple quadratic harmonic function that will serve as neumann values. More...

Detailed Description

This module contains functions to setup and solve boundary integral equations for the Laplace operator in 2D.

Function Documentation

field eval_dirichlet_linear_laplacebem2d	(	const real *	x,
		const real *	n
	)

A simple linear harmonic function that will serve as dirichlet values.

When computing the neumann data out of the dirichlet data one can use this function as test data which will generate dirichlet values of with the following values:

$f(\vec x, \, \vec n) = x_1 + x_2$

Corresponding neumann data can be generated by using eval_neumann_linear_laplacebem2d.
To build up an appropriate dirichlet data coefficient vector one needs the $ L_2$ -projection. This can be done by passing this function to projectl2_bem2d_const_avector for piecewise constant basis functions.

Parameters

x	Evaluation point.
n	Normal vector to current evaluation point.

Returns: returns the function value of $f(\vec x, \, \vec n)$ .

field eval_dirichlet_quadratic_laplacebem2d	(	const real *	x,
		const real *	n
	)

A simple quadratic harmonic function that will serve as dirichlet values.

When computing the neumann data out of the dirichlet data one can use this function as test data which will generate dirichlet values of with the following values:

$f(\vec x, \, \vec n) = x_1^2 - x_2^2$

Corresponding neumann data can be generated by using eval_neumann_quadratic_laplacebem2d.
To build up an appropriate dirichlet data coefficient vector one needs the $ L_2$ -projection. This can be done by passing this function to projectl2_bem2d_const_avector for piecewise constant basis functions.

Parameters

x	Evaluation point.
n	Normal vector to current evaluation point.

Returns: returns the function value of $f(\vec x, \, \vec n)$ .

field eval_neumann_linear_laplacebem2d	(	const real *	x,
		const real *	n
	)

A simple linear harmonic function that will serve as neumann values.

When computing the neumann data out of the dirichlet data one can use this function as test data which will generate neumann values of with the following values:

$f(\vec x, \, \vec n) = n_1 + n_2$

Corresponding dirichlet data can be generated by using eval_dirichlet_linear_laplacebem2d.
To build up an appropriate neumann data coefficient vector one needs the $ L_2$ -projection. This can be done by passing this function to projectl2_bem2d_const_avector for piecewise constant basis functions.

Parameters

x	Evaluation point.
n	Normal vector to current evaluation point.

Returns: returns the function value of $f(\vec x, \, \vec n)$ .

field eval_neumann_quadratic_laplacebem2d	(	const real *	x,
		const real *	n
	)

A simple quadratic harmonic function that will serve as neumann values.

When computing the neumann data out of the dirichlet data one can use this function as test data which will generate neumann values of with the following values:

$f(\vec x, \, \vec n) = 2 \cdot x_1 \cdot n_1 - 2 \cdot x_2 \cdot n_2$

Corresponding dirichlet data can be generated by using eval_dirichlet_quadratic_laplacebem2d.
To build up an appropriate neumann data coefficient vector one needs the $ L_2$ -projection. This can be done by passing this function to projectl2_bem2d_const_avector for piecewise constant basis functions.

Parameters

x	Evaluation point.
n	Normal vector to current evaluation point.

Returns: returns the function value of $f(\vec x, \, \vec n)$ .

pbem2d new_dlp_laplace_bem2d	(	pccurve2d	gr,
		uint	q,
		basisfunctionbem2d	basis_neumann,
		basisfunctionbem2d	basis_dirichlet,
		field	alpha
	)

Creates a new bem2d-object for computation of double layer potential matrix.

After calling this function the resulting bem-object will provide all functionality that is necessary to build up fully populated double layer potential matrix $K + \frac{1}{2} M \in \mathbb R^{\mathcal I \times \mathcal J}$ and also hmatrix or h2matrix approximation of this matrix.

Parameters

gr	Polygonal, two dimensional geometry.
q	Order of gaussian quadrature used within computation of matrix entries.
basis_neumann	Type of basis functions used for neumann data.
basis_dirichlet	Type of basis functions used for dirichlet data.
alpha	Double layer operator + 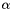$\alpha$ mass matrix.

Returns: Returns a bem-object that can compute fully populated dlp matrices $K + \frac{1}{2} M$ for the laplace equation.

pbem2d new_slp_laplace_bem2d	(	pccurve2d	gr,
		uint	q,
		basisfunctionbem2d	basis
	)

Creates a new bem2d-object for computation of single layer potential matrix.

After calling this function the resulting bem-object will provide all functionality that is necessary to build up fully populated single layer potential matrix $V \in \mathbb R^{\mathcal I \times \mathcal I}$ and also hmatrix or h2matrix approximation of this matrix.

Parameters

gr	Polygonal, two dimensional geometry.
q	Order of gaussian quadrature used within computation of matrix entries.
basis	Type of basis functions used for neumann data.

Returns: Returns a bem-object that can compute fully populated slp matrices for the laplace equation.

Functions

Detailed Description

Function Documentation